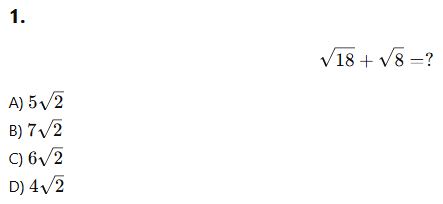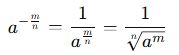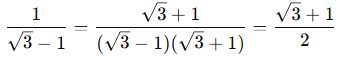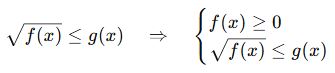AYT Matematik Köklü Sayılar Konu Anlatımı

Bu konu, sadeleştirme, rasyonel hâle getirme, denklem çözme ve grafik yorumlama gibi birçok alanda kullanılır. Özellikle AYT’de mantık isteyen sorularla test edilir.

Köklü Sayılar

🔹 Köklü İfade Nedir?

Köklü İfadenin Üslü İfade ile İlişkisi:

Bu ilişki, üslü sayılarla köklü ifadeleri birbirine çevirmede kullanılır.

🎯 Köklü Sayı Tanım Koşulları:

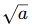• → sadece a ≥ 0 için gerçel sayı

• Tek dereceli kökler (örneğin küpkök) → her sayının kökü alınabilir

• Çift dereceli köklerde, kök içi negatifse → tanımsız (ℝ’de)

📚 Köklü Sayılar Ünitesinin Alt Başlıkları:

1. Köklü İfade Tanımı ve Özellikleri

2. Köklü – Üslü Dönüşümler

3. Köklü Sayılarda Dört İşlem

4. Sadeleştirme ve Rasyonel Hâle Getirme

5. Denklemler ve Eşitsizlikler

6. AYT Seviyesi Problemler

AYT’de Neler Sorulur?

• Sadeleştirme, karşılaştırma

• Karma işlemler (çarpanlara ayırma, rasyonelleştirme)

• Denklem çözümü

• Kök içi ve kök dışı ifadelerin değerlendirilmesi

• Sayı doğrusunda yorum, sıralama ve grafik

Köklü İfade Tanımı ve Temel Özellikleri

📘 Tanım:

🟡 Tanım Koşulları (ℝ için):

Yani çift dereceli kökün içi negatif olamaz (gerçel sayılar kümesinde).

📘 Temel Özellikler:

🔸 1. Kök ile Üs İlişkisi:

🔸 2. Kökler Çarpımı:

Örnek:

🔸 3. Kökler Bölümü:

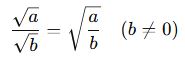
Örnek:

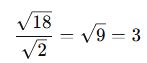
🔸 4. Kök İçine Alma – Kök Dışına Çıkarma:

• Kök dışına çıkarma:

• Kök içine alma:

​

Örnek:

​

🔸 5. Mutlak Değer Özelliği:

Örnek:

AYT’de Bu Konuda Dikkat Edilmesi Gerekenler:

• Kök içini tam kare / tam küp hâline getirmeye çalış

• Tanım kümesi ve mutlak değer ilişkisi çok çıkar

• Parantezsiz ifadelerde negatifler karışabilir

• Kare köklü ifadeler sadeleştirilmeden önce sıkıştırılır veya dışa alınır

Köklü – Üslü Dönüşümler

📘 Temel Kural:

Köklü ifadeler, uygun şekilde üslü ifadelere dönüştürülebilir. Bu da işlemleri hızlandırır ve bazı AYT sorularında çözümü kolaylaştırır.

​

Bu iki yönlü dönüşüm çok önemlidir.

🧠 Parçalayarak Düşünme:

Bu özellik sayesinde önce kök al, sonra üssü uygula veya tam tersi.

📌 Negatif ve Rasyonel Üs Birlikte:

​

Örnek:

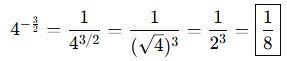
Dönüşüm Uygulamalı Örnekler

🎓 Örnek 1:

🎓 Örnek 2:

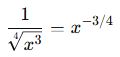
🎓 Örnek 3:

AYT’de Dikkat Edilmesi Gerekenler:

• Sınavda köklü verilip üslü hâle çevrilerek işlem istenebilir

• Üslerde işlem kolaylığı için ortak payda yapılır

• Negatif ve kesirli üs içeren ifadeler önce sadeleştirilmeli

• Mutlaka kök – üs dönüşümü alışkanlık hâline getirilmeli

Köklü Sayılarda Dört İşlem

📘 A. Toplama – Çıkarma

Köklü ifadeler, aynı kök derecesine ve aynı kök içine sahipse toplanıp çıkarılabilir.

🔸 Kural:

🎓 Örnek 1:

🎓 Örnek 2 (Sadeleştirme gerekebilir):

​

📌 Çünkü:

❌ Farklı köklü ifadeler toplanamaz:

📘 B. Çarpma

Köklü ifadelerde çarpma, hem kök dışı hem kök içi çarpılarak yapılır:

🔸 Kural:

🎓 Örnek:

📘 C. Bölme

Bölme işleminde hem kök dışı hem kök içi sadeleştirilir. Gerekirse kök rasyonelleştirilir.

🔸 Kural:

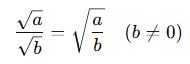
🎓 Örnek:

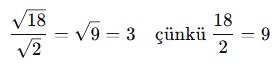
📘 D. Rasyonel Hâle Getirme

Eğer paydada köklü ifade varsa, payda kökten kurtarılır.

🔸 1. Kareköklü İfade:

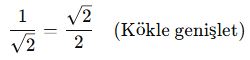
🔸 2. İki terimli köklü ifade:

​

📌 Bu işleme eşlenik ile çarpma denir.

🎯 AYT Düzeyi Karma Örnek:

AYT’de Dikkat Edilmesi Gerekenler:

• Her zaman kök içini sadeleştirerek başla

• Toplama ve çıkarma için kök içleri aynı olmalı

• Paydada kök varsa rasyonel hâle getir

• Kök dışı çarpanlar ayrı ele alınır

Sadeleştirme ve Rasyonel Hâle Getirme

📘 A. Kök İçini Sadeleştirme

Köklü ifadelerde işlem kolaylığı sağlamak için önce kök içi sadeleştirilir.

🔸 Kural:

​

Eğer a ya da b tam kare ise dışarı alınabilir.

🎓 Örnek:

📘 B. Kök Dışına Alma – Kök İçine Gönderme

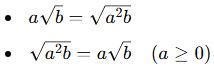
🎓 Örnek:

📘 C. Rasyonel Hâle Getirme

🔹 1. Tek Terimli Payda:

Paydada kök varsa, aynı kökle genişletilir.

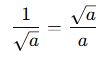
🎓 Örnek:

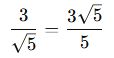
🔹 2. İki Terimli Payda – Eşlenik Kullanımı

İki terimli ifadelerde payda, eşleniğiyle çarpılarak rasyonelleştirilir.

Eşlenik = aynı terimlerin işaretlisi

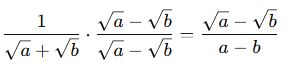
🎓 Örnek:

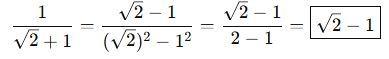
🎓 Örnek (Zorluk Artıyor):

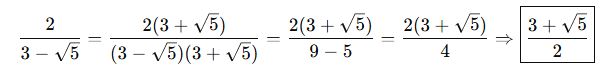
AYT’de Dikkat Edilecek Noktalar:

• Rasyonelleştirme genellikle çok adımlı sadeleştirme gerektirir

• Özellikle eşlenik kullanımı sınavda seçici sorularda çıkar

• Sonucu sade yazmayı unutma

• İşlemlerde paydalar ortaklaştırılırsa ifade daha basitleşir

Köklü Denklemler ve Eşitsizlikler

📘 A. Kökten Kurtarma Yöntemi

Köklü denklem çözümünde en çok kullanılan yöntem, her iki tarafın karesini alarak kökten kurtulmaktır.

🔸 Kural:

Ama bu işlem her zaman doğru sonuç vermeyebilir. Çünkü kare alma işlemi denklemi genişletir → yanlış (sahte) kök oluşturabilir.

Bu yüzden mutlaka bulunan çözüm, denklemde yerine yazılarak kontrol edilmelidir.

🎓 Örnek 1:

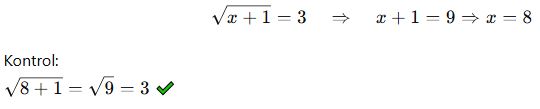
🎓 Örnek 2:

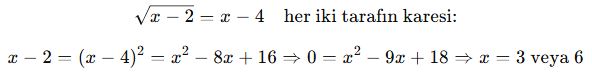
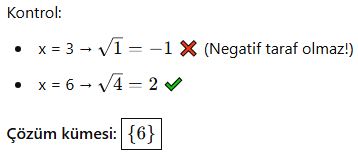
📘 B. Köklü Eşitsizlikler

Çift dereceli kökler pozitif sonuç verdiği için, eşitsizlik çözümünde karekök fonksiyonu artan gibi düşünülür.
Ancak, tanım kümesi kısıtlaması mutlaka göz önünde bulundurulmalıdır.

🔸 Kural:

​

Hem içi ≥ 0 olmalı, hem eşitsizlik sağlanmalı.

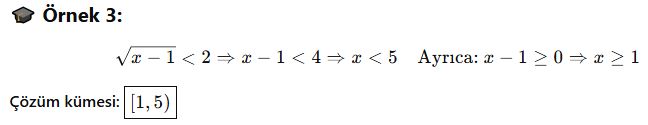
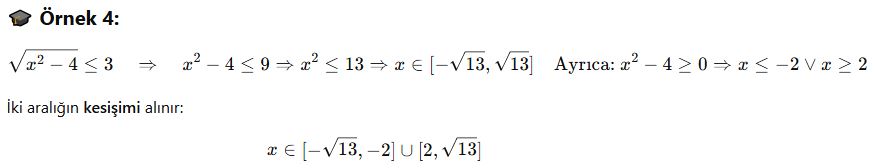
AYT’de Dikkat Edilmesi Gerekenler:

• Kare alırken denklemin her iki tarafı ≥ 0 olmalı

• Kökten kurtarma sonrası bulunan kökler denkleme geri yazılmalı

• Eşitsizliklerde tanım kümesi kesişimi unutulmamalı

• Sorular mutlak değer – kök birleşimi ile de verilebilir

• Yanlış kök tuzakları çok sık kullanılır

AYT Seviyesi Köklü Sayı Problemleri

🎯 Soru Tipi 1: Kök İçini Sadeleştir – Kıyasla

🎓 Örnek 1:

Aşağıdakilerden hangisi daha büyüktür?

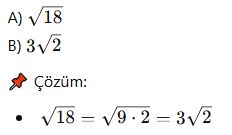
✔ Cevap: Eşit

🎯 Soru Tipi 2: Payda Rasyonelleştirme – Eşlenik Kullanımı

🎓 Örnek 2:

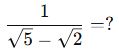
📌 Eşlenik ile çarp:

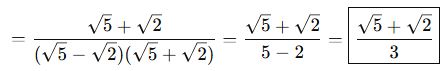
🎯 Soru Tipi 3: Denklem Kur – Kökten Kurtul

🎓 Örnek 3:

eşitliğini sağlayan x değeri kaçtır?

📌 Kare al:

​​

📌 Kökleri denkleme yazıp kontrol et!
Gerçel sayı aralığında yalnızca pozitif sonuç sağlar.

🎯 Soru Tipi 4: Tanım Kümesi – Koşullu Soru

🎓 Örnek 4:

🎯 Soru Tipi 5: Sıralama Soruları

🎓 Örnek 5:

Aşağıdaki sayıları sıralayınız:

​

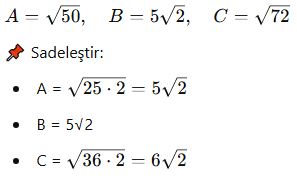
Sıralama:

AYT’de Dikkat Edilecek Noktalar:

• Kök içlerini tam kare/küp hâline getir

• Tanım kümesine dikkat et

• Payda rasyonelleştirme işlemlerinde eşlenik kritik

• Kök dışına çıkarma – kök içine alma işlem kolaylığı sağlar

• Sahte kök tuzağına düşmemek için daima kontrol yap

AYT Köklü Sayılar Deneme Testi (10 Soru)