AYT Matematik Üslü Sayılar Konu Anlatımı ve Örnek Sorular

AYT Matematik Üslü Sayılar

📘 Üslü Sayı Nedir?

Bir sayının kendisinin tekrar tekrar çarpılması işlemine üs alma denir.

Matematiksel olarak:

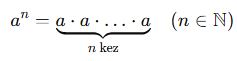
Burada:

• a → taban (base)

• n → üs (exponent)

• aⁿ → üslü ifade

🔍 Tanım Örnekleri:

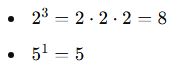
🔧 Üslü Sayılarda Bilinmesi Gerekenler

📌 Temel Özellikler:

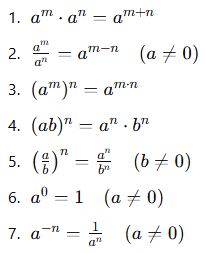
📌 Sayıların Üslü Haliyle İfadesi:

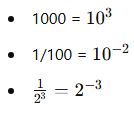
🧠 AYT’de Neden Önemli?

• Karmaşık ifadeleri sadeleştirmede kullanılır

• Logaritma, polinom, türev ve integral gibi konuların altyapısını oluşturur

• Sorular, genellikle özellikleri tanıyıp uygulamayı test eder

• Negatif üs, rasyonel üs ve köklü ifadelerle karışık ifadeler sorulur

📚 Ünitedeki Alt Başlıklar:

1. Üslü Sayı Tanımı ve Temel Özellikleri

2. Negatif ve Sıfır Kuvvet

3. Rasyonel (Kesirli) Üsler

4. Üslü İfadelerde Dört İşlem

5. Karışık Üslü Denklem ve Eşitsizlikler

6. AYT Seviyesinde Problem Çözüm Yöntemleri

Üslü Sayı Tanımı ve Temel Özellikleri

📘 Tanım:

Bir sayının kendisinin n kez çarpılması işlemine üslü sayı denir.

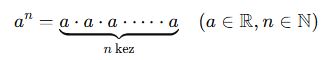
Burada:

• a: taban

• n: üs

• aⁿ: üslü ifade

📌 Üslü Sayılarda Temel Kurallar

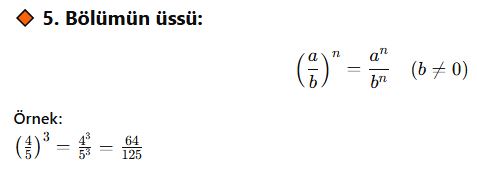
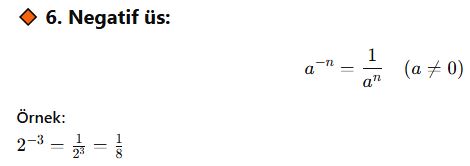
AYT Düzeyinde Dikkat Edilmesi Gerekenler:

• Tabanlar aynıysa üstel işlem kolaylaşır, ama farklıysa dikkatli olun

• Negatif ve sıfır kuvvet sıkça tuzak olarak sorulur

• Parantez kullanımına çok dikkat edin:
  

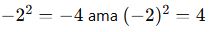
• Rasyonel ve negatif üsler bir sonraki alt başlıkta genişleyecek

Negatif ve Sıfır Kuvvet Özellikleri

🔸 A. Negatif Kuvvet

📘 Tanım:

Bir sayının negatif kuvveti, o sayının pozitif kuvvetinin 1 bölü halidir:

🎯 Sık Yapılan Hata:

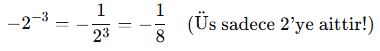
Ama

Parantez farkı çok önemli!

🔸 B. Sıfır Kuvvet

📘 Tanım:

Bir sayının sıfırıncı kuvveti her zaman 1’dir. (0 hariç)

📌 Soru Tarzı – Seçiciler:

Örnek:

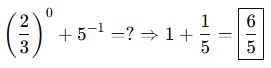
🧠 AYT Düzeyinde Dikkat Et:

• Negatif üs görürsen mutlaka pozitife çevir

• Sıfır kuvvet sorularında tabanın sıfır olup olmadığını kontrol et

• İşlem sırası: önce üssü al, sonra çarp veya topla

• Parantez unutulursa işaret hatası olur

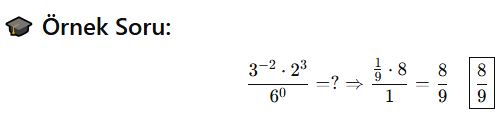
Rasyonel (Kesirli) Üsler ve Köklerle İlişkisi

📘 Tanım:

Bir sayının rasyonel (kesirli) üssü, aslında o sayının kök şeklinde ifade edilmesidir.

Yani:

• Üstteki pay (m) → üs

• Alttaki payda (n) → kök derecesidir

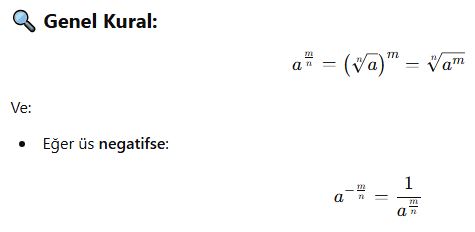
🎯 AYT’de Sıklıkla Kullanılan Pratikler:

• Kök içinden üslü ifadeye, üslü ifadeden köke geçiş

• İfadeyi sadeleştirmek için üsleri aynı tabanda toplamak/çıkarmak

• Üssü karşılaştırarak büyüklük/küçüklük tespiti

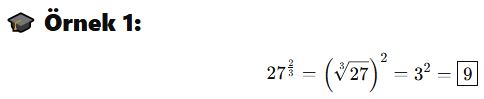
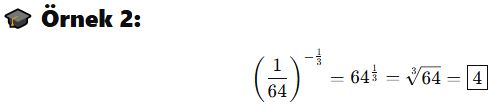
AYT’de Dikkat Edilmesi Gerekenler:

• Negatif üs varsa ters çevir

• Rasyonel üslerde önce kök al, sonra kuvvet uygula (ya da tersi)

• Sadeleştirme ve karşılaştırma yaparken aynı tabana getirmeye çalış

• İfade içinde hem üs hem kök varsa, açık yazıp işlem yap

• Sınavda logaritma, polinom gibi konularla birlikte çıkabilir

Üslü İfadelerde Dört İşlem ve Sadeleştirme Teknikleri

📘 A. Toplama ve Çıkarma İşlemi

🟡 Kural:
Toplama ve çıkarma ancak taban ve üs aynıysa yapılabilir.
Tıpkı cebirsel terimlerdeki gibi düşün.

🎓 Örnek:

❗ Not:

Üs farklıysa ya da taban farklıysa toplama-çıkarma yapılamaz!

📘 B. Çarpma İşlemi

🟢 Kural:
Aynı tabanlı çarpma → üsler toplanır:

Farklı tabanlı ama aynı üsse sahipse → üs dışına alınabilir:

🎓 Örnek:

📘 C. Bölme İşlemi

🔵 Kural:
Aynı tabanlı bölme → üsler çıkarılır:

🎓 Örnek:

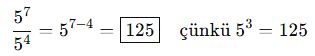
📘 D. Üssün Üssü

🟣 Kural:

🎓 Örnek:

📘 E. Üslü İfade Sadeleştirme Örnekleri

Örnek 1:

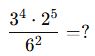
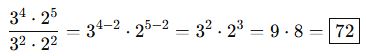
Örnek 2:

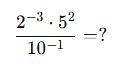
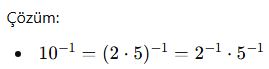
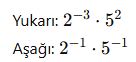
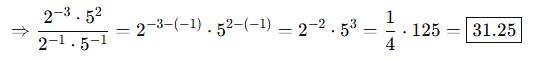
AYT’de Dikkat Edilmesi Gerekenler:

• Sadeleştirme yaparken önce tabanlara göre grupla

• İşaretler ve negatif üsler için dikkatli ol

• Aynı taban ve aynı üs varsa sadeleştirme çok hızlanır

• Toplama-çıkarma işlemleri ancak terimler özdeşse yapılabilir

• Parantez yoksa üs sadece yanındaki sayı içindir!

Üslü Sayılarda Denklem ve Eşitsizlik Çözümü

📘 A. Üslü Denklemler

Amaç: Üslü ifadeyi sadeleştirerek tabanları eşitlemek ve sonra üsleri karşılaştırmak.

🔸 Kural:

Eğer

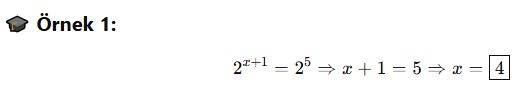
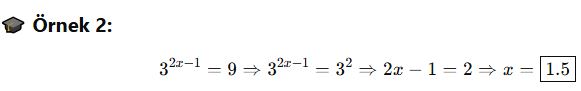
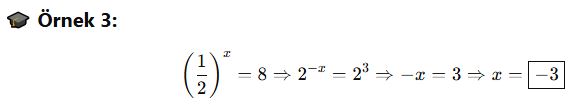
🧠 Tabanlar eşit değilse?

• Sayıları üslü ifadeye çevir

• Tabanları eşitle, ya da logaritma bilgisiyle ilerle (AYT için)

📘 B. Üslü Eşitsizlikler

Aynı tabanlı üslü ifadelerde, üsler arasında da aynı yönlü karşılaştırma yapılabilir.

🔸 Pozitif Taban, a > 1 ise:

🔸 0 < a < 1 ise:

Ters yönlü karşılaştırma:

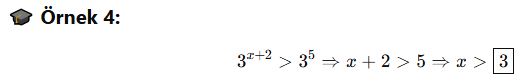
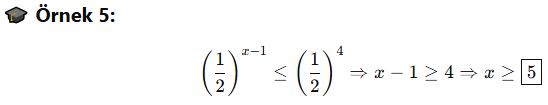
📌 Çünkü taban 0 < a < 1 olduğunda eşitsizlik yönü değişir.

AYT’de Dikkat Edilmesi Gerekenler:

• Tabanlar eşitse → üsleri karşılaştır

• Tabanlar farklıysa → üslü ifadeye çevir ve eşitle

• Taban 0 < a < 1 olduğunda eşitsizlik yönü değişir!

• Denklem ve eşitsizlik iç içe geldiyse önce sadeleştir

🎯 Soru Tarzları:

• “a^x = b^y ise, x kaçtır?”

• “Üsler verilmiş, tabanları bul”

• “Grafik üzerinde üslü fonksiyonun değeri yorumlanır”

• “Sıralama soruları” → çok çıkar

Üslü İfadelerle AYT Seviyesi Problem Çözümü

🎯 Soru Tipi 1: Taban ve Üs Arasındaki İlişki

🎓 Örnek 1:

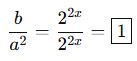
🎯 Soru Tipi 2: Üslü İfadelerle Denklem Kurma

🎓 Örnek 2:

Bir bakterinin sayısı her 2 saatte bir iki katına çıkıyor. Başlangıçta 50 bakteri varsa, 8 saat sonunda kaç bakteri olur?

📌 Çözüm:

• Her 2 saatte bir → 4 defa iki katına çıkar

🎯 Soru Tipi 3: Karşılaştırma ve Sıralama

🎓 Örnek 3:

Hangisi daha büyüktür?

🎯 Soru Tipi 4: Üslü Denklemle Tanımsızlık ve Koşul

🎓 Örnek 4:

🎯 Soru Tipi 5: Parantez Oyunu / İşaret Tuzakları

🎓 Örnek 5:

Aşağıdakilerden hangisi doğrudur?

AYT’de Dikkat Edilecekler:

• Görünüşü karmaşık sorular genelde temel kurallara dayanır

• Taban ve üs ilişkisini iyi yorumlamak gerekir

• Bir ifadeyi hem rasyonel üs hem köklü ifade olarak düşünebilmelisin

• Sorularda mantık, işlem hızı ve dikkat birlikte ölçülür

AYT Üslü Sayılar Değerlendirme Testi (10 Soru)

1.

A) 3
B) 4
C) 5
D) 6

2.

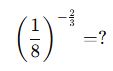
A) 4
B) 8
C) 16
D) 64

3.

eşitliğini sağlayan x değeri kaçtır?

A) 0
B) 1
C) 2
D) 3

4.

eşitliğini sağlayan x değeri kaçtır?

A) 0
B) 1
C) 2
D) 3

6.

olduğuna göre, x ile y arasındaki ilişki nedir?

A) x < y
B) x > y
C) x = y
D) Karşılaştırılamaz

7.

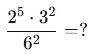
A) 2
B) 4
C) 8
D) 16

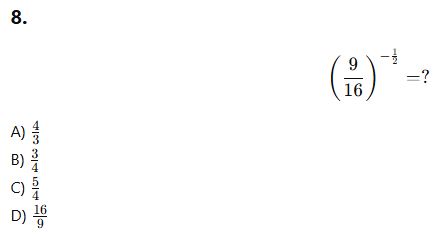
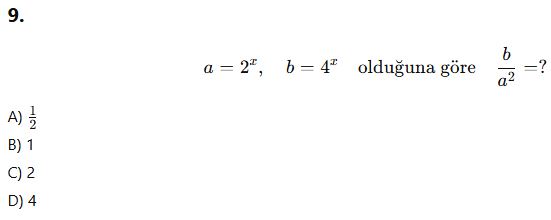
10.

Bir hücre, her 3 saatte bir 3 katına çıkıyor.
Başlangıçta 5 hücre varsa, 9 saat sonra kaç hücre olur?

A) 45
B) 81
C) 135
D) 405