TYT Matematik EBOB – EKOK Konu Anlatımı ve Örnek Sorular

EBOB – EKOK Konu Anlatımı

Matematikte EBOB (En Büyük Ortak Bölen) ve EKOK (En Küçük Ortak Kat) kavramları, sayıların ortak bölenlerini ve ortak katlarını belirlemek için kullanılır. TYT Matematik’te sıkça karşılaşılan bu konu, özellikle bölme bölünebilme, kesirler ve problemler gibi alanlarda temel bir rol oynar.

EBOB, iki veya daha fazla sayının ortak bölenleri arasındaki en büyük değeri ifade ederken, EKOK bu sayıların ortak katları arasındaki en küçük değeri temsil eder. Bu konu, kesirlerde işlemler, zaman hesaplamaları ve problem çözme gibi birçok farklı alanda kullanılmaktadır.

Bu bölümde, EBOB ve EKOK’un nasıl hesaplandığını, hangi yöntemlerin kullanıldığını ve konuya ilişkin problem çözme tekniklerini detaylıca ele alacağız.

Hazırsanız, konuyu adım adım keşfetmeye başlayalım! 🚀📚

EBOB (En Büyük Ortak Bölen)

EBOB, iki veya daha fazla sayının ortak bölenleri arasındaki en büyük sayıdır.

EBOB Bulma Yöntemleri:

1. Bölenleri Listeleme Yöntemi

   • Sayıların bölenleri tek tek yazılır.
   • Ortak olan bölenler belirlenir.
   • En büyük ortak bölen bulunur.

2. Asal Çarpanlara Ayırma Yöntemi

   • Sayılar asal çarpanlarına ayrılır.
   • Ortak olan asal çarpanlar belirlenir.
   • Ortak çarpanların çarpımı alınır.

Örnek 1 – Bölenleri Listeleme Yöntemi:

18 ve 24’ün EBOB’unu bulalım.

• 18’in bölenleri: 1, 2, 3, 6, 9, 18
• 24’ün bölenleri: 1, 2, 3, 4, 6, 8, 12, 24
• Ortak Bölenler: 1, 2, 3, 6
• En Büyük Ortak Bölen (EBOB): 6

Örnek 2 – Asal Çarpanlara Ayırma Yöntemi:

30 ve 45’in EBOB’unu bulalım.

• 30 = 2 × 3 × 5
• 45 = 3 × 3 × 5
• Ortak çarpanlar: 3 ve 5
• EBOB = 3 × 5 = 15

EBOB, en fazla bölebilen en büyük sayıdır.

EKOK (En Küçük Ortak Kat)

EKOK, iki veya daha fazla sayının ortak katları arasındaki en küçük sayıdır.

EKOK Bulma Yöntemleri:

1. Katları Listeleme Yöntemi

   • Sayıların katları tek tek yazılır.
   • Ortak olan katlar belirlenir.
   • En küçük ortak kat bulunur.

2. Asal Çarpanlara Ayırma Yöntemi

   • Sayılar asal çarpanlarına ayrılır.
   • Tüm asal çarpanlar alınır (ortak olanlar sadece bir kez yazılır).
   • Çarpım sonucu EKOK bulunur.

Örnek 1 – Katları Listeleme Yöntemi:

6 ve 8’in EKOK’unu bulalım.

• 6’nın katları: 6, 12, 18, 24, 30, 36, 42, 48, …
• 8’in katları: 8, 16, 24, 32, 40, 48, 56, …
• Ortak Katlar: 24, 48, …
• En Küçük Ortak Kat (EKOK) = 24

Örnek 2 – Asal Çarpanlara Ayırma Yöntemi:

15 ve 20’nin EKOK’unu bulalım.

• 15 = 3 × 5
• 20 = 2 × 2 × 5
• Tüm asal çarpanları alalım: 2 × 2 × 3 × 5
• EKOK = 60

EKOK, en küçük ortak katı veren en küçük sayıdır.

EBOB ve EKOK ile İlgili Problemler

Örnek 1: EBOB Problemi (Öklid Algoritması Kullanımı)

Ali ve Ayşe’nin 18 ve 24 cm uzunluğunda ipleri vardır. Bu ipleri eşit uzunlukta parçalara bölmek istiyorlar. Her bir parça kaç cm uzunluğunda olabilir?

Çözüm:

• EBOB(18,24) = 6
• Her bir parça en fazla 6 cm olabilir. ✅

Örnek 2: EKOK Problemi (En Küçük Ortak Zaman Hesaplama)

Bir tren 15 dakikada, bir otobüs ise 20 dakikada bir duraktan geçiyor. İkisi birlikte en erken kaç dakika sonra tekrar duraktan aynı anda geçer?

Çözüm:

• EKOK(15,20) = 60
• Cevap: 60 dakika sonra. ✅

Örnek 3: EBOB-EKOK Bağlantılı Problem

İki sayı veriliyor: A ve B

• EBOB(A, B) = 12
• EKOK(A, B) = 180

Bu durumda A × B çarpımı kaçtır?

Çözüm:
Matematikte şu formül geçerlidir:

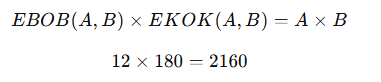
Cevap: 2160 ✅

• EBOB, iki veya daha fazla sayının ortak bölenleri arasındaki en büyük sayıdır.
• EKOK, iki veya daha fazla sayının ortak katları arasındaki en küçük sayıdır.
• EBOB, sayıların bölünebilirlik kurallarında; EKOK ise tekrar eden olaylarda (zaman, sıklık) sıkça kullanılır.
• EBOB ve EKOK formülü:

TYT Matematik – EBOB ve EKOK Ünitesi Testi

Aşağıdaki test, EBOB ve EKOK konusunu pekiştirmenize yardımcı olacaktır. Soruları dikkatlice okuyup en doğru seçeneği işaretleyin.

1. 24 ve 36 sayılarının EBOB’u kaçtır?

A) 6
B) 8
C) 12
D) 18

2. 18 ve 30 sayılarının EKOK’u kaçtır?

A) 60
B) 90
C) 120
D) 150

3. İki sayının çarpımı 360, EBOB’u 12 ise EKOK’u kaçtır?

A) 20
B) 30
C) 36
D) 40

4. 40 ve 48 sayılarının EBOB ve EKOK değerleri çarpıldığında hangi sonuç elde edilir?

A) 960
B) 1920
C) 2400
D) 3840

5. İki farklı doğal sayının EBOB’u 7, EKOK’u 210’dur. Bu iki sayıdan biri 21 olduğuna göre diğer sayı kaçtır?

A) 35
B) 42
C) 49
D) 63

6. 15 ve 20 dakikada bir hareket eden iki otobüs, sabah 06:00’da aynı anda hareket ediyor. İkisi tekrar en erken saat kaçta aynı anda hareket eder?

A) 06:30
B) 07:00
C) 07:30
D) 08:00

7. Bir markette 36 ve 54 şişelik iki farklı meyve suyu paketi bulunmaktadır. Bu paketlerden eşit büyüklükte gruplar oluşturulacaktır. Her grupta en fazla kaç şişe olabilir?

A) 6
B) 9
C) 12
D) 18

8. Bir spor salonunda A egzersizi 12 dakikada bir, B egzersizi 15 dakikada bir yapılmaktadır. A ve B egzersizleri aynı anda başladıktan sonra en erken kaç dakika sonra tekrar birlikte yapılır?

A) 30
B) 45
C) 60
D) 90

9. A ve B iki doğal sayıdır. EBOB(A, B) = 5 ve EKOK(A, B) = 60 ise, A × B çarpımı kaçtır?

A) 200
B) 250
C) 300
D) 350

10. 20 ve 50 sayılarına bölünebilen en küçük sayı kaçtır?

A) 100
B) 150
C) 200
D) 250

Cevap Anahtarı

1. C
2. A
3. C
4. B
5. B
6. B
7. C
8. C
9. C
10. C

Bu testi çözüp kendinizi değerlendirebilirsiniz. Hatalı olduğunuz soruları tekrar gözden geçirmeyi unutmayın! 🚀📚