TYT Matematik Veri ve İstatistik Konu Anlatımı

Matematik, günlük yaşamda karşımıza çıkan olayları anlamlandırmak ve düzenlemek için kullanılan güçlü bir araçtır. Özellikle verilerin toplanması, düzenlenmesi, yorumlanması ve analiz edilmesi, istatistik bilim dalının temelini oluşturur. İstatistik, birçok farklı alanda kullanılır: Eğitimde sınav sonuçlarını değerlendirmek, ekonomide enflasyon oranlarını incelemek, sağlık sektöründe hastalık verilerini analiz etmek gibi pek çok alanda istatistikten faydalanılır.

Bu ünitede, veri ve veri türleri, veri toplama ve düzenleme, merkezi eğilim ölçüleri (aritmetik ortalama, medyan, mod), merkezi dağılım ölçüleri (açıklık, standart sapma, varyans) ve grafik yorumlama gibi temel istatistik kavramlarını öğreneceğiz. Konuları adım adım örneklerle açıklayarak, verileri nasıl analiz edeceğimizi ve yorumlayacağımızı öğreneceğiz.

1. Veri ve Veri Türleri

Veri, belirli bir konu hakkında elde edilen ve analiz edilerek anlam çıkarılabilen sayısal veya sözel bilgilerdir. Veriler günlük hayatımızda sıkça karşımıza çıkar. Örneğin, bir okulun öğrencilerinin boy uzunlukları veya bir mağazanın aylık satış rakamları birer veridir. Veriler, belirli kurallara göre sınıflandırılır ve analiz edilir.

Veriler nitel (kalitatif) ve nicel (kantitatif) olmak üzere ikiye ayrılır:

• Nitel (Kalitatif) Veriler: Sayılarla ifade edilemeyen, gözleme dayalı verilerdir. Örneğin, kişilerin göz rengi, meslekleri veya hobileri nitel verilerdir.
• Nicel (Kantitatif) Veriler: Sayılarla ifade edilebilen ve ölçülebilen verilerdir. Örneğin, bir kişinin kilosu, yaşadığı şehirdeki sıcaklık veya sınavda aldığı puan nicel verilerdir.
  • Sürekli Veri: Ölçülebilen ve belirli bir aralık içinde sonsuz değer alabilen verilerdir. Örneğin, boy uzunluğu (167,5 cm gibi ara değerler de mümkündür).
  • Süreksiz Veri: Sayılabilen ve yalnızca belirli değerler alabilen verilerdir. Örneğin, bir sınıftaki öğrenci sayısı.

Örnek: Bir okulda öğrencilerin en sevdikleri spor dalları hakkında bir anket yapılıyor. Sonuçlar şu şekildedir:

• 15 öğrenci basketbolu seviyor.
• 20 öğrenci futbolu seviyor.
• 10 öğrenci yüzmeyi seviyor.

Bu veriler nitel veridir çünkü spor dalları sayılarla ölçülemez. Ancak eğer öğrencilerin boy uzunlukları veya ağırlıkları kaydedilseydi, bu nicel veri olurdu.

2. Veri Toplama ve Düzenleme

Veriler, belirli yöntemlerle toplanır ve düzenlenerek analiz edilir. Veri toplama sürecinde dikkat edilmesi gereken bazı noktalar şunlardır:

• Doğru ve Güvenilir Veri Toplama: Verilerin doğru kaydedilmesi gerekir.
• Verilerin Düzenlenmesi: Ham veriler tablolar halinde gösterilir.
• Frekans ve Sıklık Tabloları: Verilerin kaç kez tekrar ettiğini gösteren tablolar hazırlanır.

Örnek: Bir sınıftaki öğrencilerin en çok tercih ettiği dersi gösteren bir tablo oluşturalım:

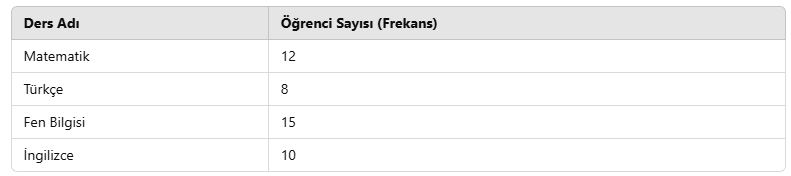
Bu tablo, öğrencilerin en çok ilgi duyduğu dersleri göstermektedir. En fazla tercih edilen ders Fen Bilgisi (15 öğrenci) iken, en az tercih edilen ders Türkçe (8 öğrenci) olmuştur.

3. Merkezi Eğilim Ölçüleri

Merkezi eğilim ölçüleri, bir veri grubunun genel yapısını özetleyen ölçülerdir. Bunlar:

• Aritmetik Ortalama: Verilerin toplamının, veri sayısına bölünmesiyle elde edilir.
• Medyan (Ortanca): Veriler küçükten büyüğe sıralandığında ortada kalan değerdir.
• Mod (Tepe Değer): Bir veri grubunda en çok tekrar eden değerdir.

Örnek: Bir sınıftaki 5 öğrencinin sınav notları: 70, 85, 90, 75, 85

• Aritmetik Ortalama: (70 + 85 + 90 + 75 + 85) / 5 = 81
• Medyan: Sıralanmış veri: 70, 75, 85, 85, 90 → Ortanca değer: 85
• Mod: En çok tekrar eden değer: 85

4. Merkezi Dağılım Ölçüleri

Bir veri grubundaki değerlerin birbirine olan dağılımını gösteren ölçülerdir.

• Açıklık: En büyük ve en küçük değer arasındaki farktır.
• Standart Sapma: Verilerin ortalamaya olan uzaklıklarının bir ölçüsüdür.

Örnek: Bir sınıftaki 6 öğrencinin boy uzunlukları: 160 cm, 165 cm, 170 cm, 175 cm, 180 cm, 185 cm

• Açıklık: 185 – 160 = 25 cm
• Standart sapma: Daha ayrıntılı bir hesaplama gerektirir ve ortalamadan sapmalar hesaplanarak bulunur.

5. Grafik Yorumlama

Verileri görselleştirmenin en etkili yollarından biri grafik kullanımıdır. En yaygın kullanılan grafik türleri şunlardır:

• Çubuk Grafikleri: Kategorik verileri karşılaştırmak için kullanılır.
• Daire Grafikleri: Verileri yüzde olarak göstermeye uygundur.
• Histogramlar: Sürekli verileri gruplandırarak göstermek için kullanılır.

Örnek: Bir okulun öğrencilerinin en sevdikleri spor dalları aşağıdaki gibi dağılım göstermektedir

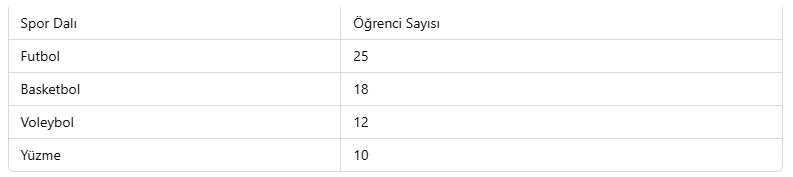
Bu veriler çubuk grafik veya daire grafik ile gösterilebilir.

Veri – İstatistik 10 Soruluk Test

1. Aşağıdakilerden hangisi nitel veriye örnektir?
   a) Bir okulun öğrenci sayısı
   b) Öğrencilerin göz renkleri
   c) Sınıftaki öğrencilerin yaşları
   d) Bir mağazanın günlük satış rakamları
2. Aşağıdakilerden hangisi sürekli veriye örnektir?
   a) Bir sınıftaki öğrenci sayısı
   b) Bir kişinin kilosu
   c) Bir okulun öğrenci sayısı
   d) Bir ilçedeki okul sayısı
3. 5, 10, 15, 20, 25 veri setinin aritmetik ortalaması kaçtır?
4. 7, 8, 10, 10, 12, 15 veri setinin modu nedir?
5. 60, 65, 70, 75, 80, 85 veri setinin açıklığı kaçtır?
6. Bir veri grubunda en çok tekrar eden değere ne ad verilir?
7. Aşağıdaki grafik türlerinden hangisi yüzde dağılım göstermek için kullanılır?
   a) Çubuk Grafik
   b) Daire Grafiği
   c) Histogram
   d) Çizgi Grafiği
8. 5, 10, 15, 20, 25 veri setinde medyan nedir?
9. Açıklık nasıl hesaplanır?
10. Histogram hangi tür verileri göstermek için kullanılır?

 Cevap Anahtarı

1. Aşağıdakilerden hangisi nitel veriye örnektir? b) Öğrencilerin göz renkleri
2. Aşağıdakilerden hangisi sürekli veriye örnektir? b) Bir kişinin kilosu
3. 5, 10, 15, 20, 25 veri setinin aritmetik ortalaması kaçtır? 15
4. 7, 8, 10, 10, 12, 15 veri setinin modu nedir? 10
5. 60, 65, 70, 75, 80, 85 veri setinin açıklığı kaçtır? 25
6. Bir veri grubunda en çok tekrar eden değere ne ad verilir? Mod
7. Aşağıdaki grafik türlerinden hangisi yüzde dağılım göstermek için kullanılır? b) Daire Grafiği
8. 5, 10, 15, 20, 25 veri setinde medyan nedir? 15
9. Açıklık nasıl hesaplanır? En büyük değer – En küçük değer
10. Histogram hangi tür verileri göstermek için kullanılır? Sürekli veriler