Matematikte tam sayılar, doğal sayıları da kapsayan geniş bir kümedir, ancak tam sayılar her zaman iki sayı arasındaki tüm değerleri ifade edemez. İşte bu noktada rasyonel sayılar devreye girer. Günlük hayatta birçok ölçüm, oran, kesir ve bölme işlemi rasyonel sayılar ile ifade edilir.
İçindekiler
Rasyonel Sayılar Konu Anlatımı
Bu ünitede, rasyonel sayıların tanımını yapacak, sayı doğrusunda nasıl gösterileceğini öğrenecek, ondalık gösterimleri inceleyecek ve rasyonel sayıları sıralayıp karşılaştırmayı öğreneceğiz.
Şimdi ilk konumuz olan “Rasyonel Sayılar ve Rasyonel Sayıların Sayı Doğrusunda Gösterilmesi” ile başlayalım.
Rasyonel Sayılar ve Rasyonel Sayıların Sayı Doğrusunda Gösterilmesi
Rasyonel Sayı Nedir?
Bir rasyonel sayı, a ve b birer tam sayı olmak üzere, b ≠ 0 koşuluyla a/b biçiminde yazılabilen bir sayıdır.
✔ Örnek Rasyonel Sayılar:
- 3/4, -5/2, 7, -8/1, 0, 2.5
✔ Tam Sayılar da Rasyonel Sayıdır!
Bir tam sayıyı bölme işlemi şeklinde yazabiliyorsak, bu sayı da rasyoneldir. Örneğin:
- 5 = 5/1,
- -2 = -2/1,
- 0 = 0/1
Bütün tam sayılar paydasına 1 eklenerek rasyonel sayı olarak gösterilebilir.
Rasyonel Sayıların Sayı Doğrusunda Gösterilmesi
Sayı doğrusu, sayıları büyükten küçüğe ya da küçükten büyüğe doğru sıralamak için kullanılan bir araçtır. Rasyonel sayıları sayı doğrusunda göstermek için aşağıdaki adımları takip edebiliriz:
1️⃣ Öncelikle rasyonel sayıyı kesir şeklinde yazın.
- Örneğin 3/4 sayısını gösterelim.
2️⃣ Payda, kaç eş parçaya böleceğimizi gösterir.
- 3/4’ü göstermek için, 0 ile 1 arasını 4 eşit parçaya böleriz.
3️⃣ Pay, bu bölmelerin kaçıncısını seçtiğimizi gösterir.
- 3/4, sıfırdan başlayarak üçüncü bölmeye denk gelir.
📌 Örnek:
-5/3 sayısını gösterelim.
- -5/3, sıfırın sol tarafında yer alır.
- Önce 0 ile -1 arasını 3 parçaya böleriz.
- -5/3, -1’den sonra bir bölme daha ileride olur.
📌 Örnek:
1.5 sayısı sayı doğrusunda nasıl gösterilir?
- 1.5 = 3/2 olduğu için, 0 ile 1 arasını 2’ye böleriz ve 3. bölmeyi işaretleriz.
Rasyonel Sayıların Ondalık Gösterimi
Rasyonel sayılar, kesir biçiminde yazılabildiği gibi ondalık gösterimle de ifade edilebilir. Günlük hayatta birçok ölçüm, alışverişte kullanılan fiyatlar ve yüzdelik ifadeler ondalık gösterimle yazılır.
Bir rasyonel sayı kesir biçiminden ondalık gösterime dönüştürülürken pay paydaya bölünerek işlem yapılır.
📌 Örnek:
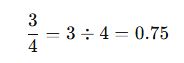
Sonuç: 3/4 kesri, ondalık gösterimde 0.75 olarak yazılır.
1. Kesirleri Ondalık Gösterime Dönüştürme
Rasyonel sayıları iki farklı türde ondalık gösterimle ifade edebiliriz:
✅ A) Sonlu Ondalık Gösterimler
✅ B) Sonsuz (Devirli) Ondalık Gösterimler
A) Sonlu Ondalık Gösterimler
Bir kesrin paydası 10, 100, 1000 gibi 10’un kuvvetleri olacak şekilde genişletilirse, kesir sonlu ondalık gösterim olarak yazılabilir.
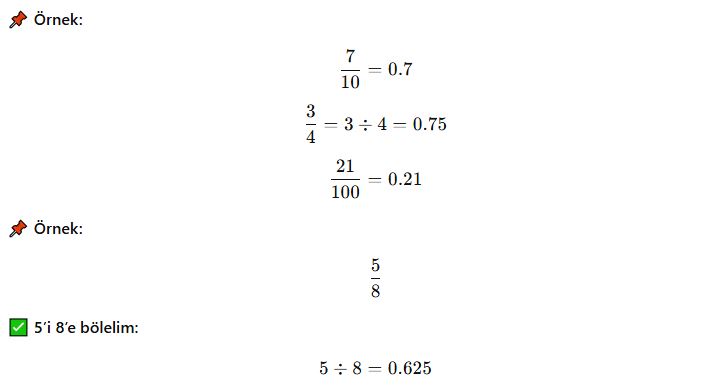
Sonuç: 5/8 = 0.625 olarak yazılır.
B) Sonsuz (Devirli) Ondalık Gösterimler
Bazı kesirler tam bölünemez ve sonsuza kadar devam eden bir ondalık sayıya dönüşür. Ancak, belirli bir tekrar eden basamak vardır.
Bu tür ondalık gösterimlere “devirli ondalık gösterim” denir.

Devirli kısım, tekrar eden rakamdır ve üstüne çizgi konularak gösterilir.
Özet
✔ Sonlu ondalık gösterim: Kesir bölündüğünde işlem biter. (Örn: 3/4 = 0.75)
✔ Devirli ondalık gösterim: Kesir bölündüğünde tekrar eden rakamlar oluşur. (Örn: 1/3 = 0.33333333)
📌 Örnek Problemler
-
Aşağıdaki kesirleri ondalık gösterim olarak yazınız:
a) 5/8
b) 7/9
c) 2/5 -
Hangi sayı sonlu ondalık gösterime sahiptir?
A) 1/4
B) 7/11
C) 5/9
D) 3/7
Devirli Olan ve Olmayan Ondalık Gösterimlerin Rasyonel Sayı Olarak İfade Edilmesi
Bazı ondalık sayılar sonlu iken bazıları sonsuz devirli olabilir. Peki, sonsuz devirli ondalık sayılar nasıl rasyonel sayıya çevrilir? Bu konuyu detaylıca ele alalım.
1. Sonlu Ondalık Gösterimleri Rasyonel Sayıya Çevirme
Sonlu ondalık gösterimler doğrudan kesir şeklinde yazılabilir.
📌 Örnekler:
- 0.6 = 6/10 = 3/5
- 1.25 = 125/100 = 5/4
- 2.75 = 275/100 = 11/4
Burada, ondalık kısım 10’un kuvveti şeklinde paydaya eklenir ve gerekirse sadeleştirilir.
📌 Örnek:
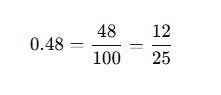
2. Devirli Ondalık Gösterimleri Rasyonel Sayıya Çevirme
Sonsuz tekrarlayan (devirli) ondalık sayılar denklem yöntemi ile rasyonel sayıya çevrilebilir.
📌 Örnek 1:
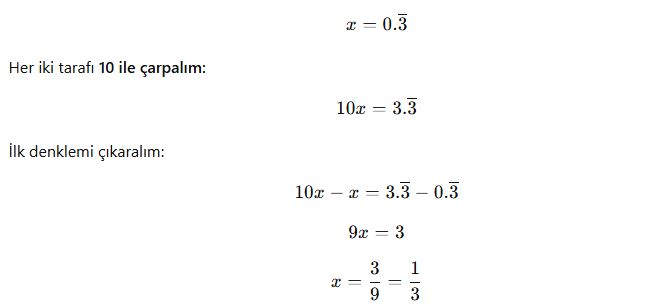
📌 Örnek 2:

📌 Örnek 3:

Özet
✔ Sonlu ondalık gösterimler doğrudan kesire çevrilebilir.
✔ Devirli ondalık gösterimler denklem yöntemiyle kesir olarak yazılır.
✔ Kesirler sadeleştirilerek en sade hali bulunur.
Rasyonel Sayıları Sıralama ve Karşılaştırma
Rasyonel sayıları büyükten küçüğe veya küçükten büyüğe sıralamak ya da hangi sayının daha büyük olduğunu belirlemek için bazı yöntemler kullanılır.
Bu yöntemleri inceleyelim:
1. Paydaları Eşitleyerek Karşılaştırma
İki veya daha fazla kesir sıralanırken, paydalar eşit hale getirilir ve payları karşılaştırılır.
📌 Örnek:

2. Ondalık Gösterime Çevirerek Karşılaştırma
Bazı durumlarda kesirleri ondalık gösterime çevirerek sıralamak daha kolay olabilir.
📌 Örnek:

3. Sayı Doğrusunda Göstererek Karşılaştırma
Rasyonel sayıları sayı doğrusunda göstererek hangisinin daha büyük olduğunu belirleyebiliriz.
📌 Örnek:
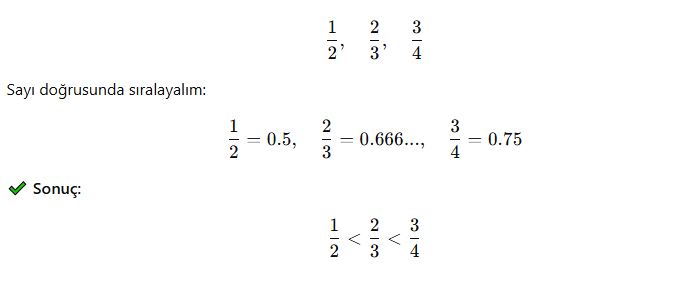
4. Negatif Rasyonel Sayıları Karşılaştırma
Negatif rasyonel sayılar küçüktür, çünkü negatif sayılar büyüdükçe değeri küçülür.
📌 Örnek:

5. Büyükten Küçüğe veya Küçükten Büyüğe Sıralama
📌 Örnek:
Aşağıdaki kesirleri küçükten büyüğe sıralayalım:
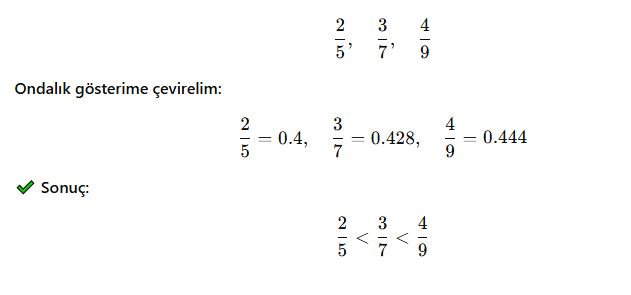
Özet
✔ Paydalar eşitlenerek karşılaştırma yapılabilir.
✔ Ondalık gösterime çevirmek sıralamayı kolaylaştırır.
✔ Negatif sayılar için sıralama ters işler.
✔ Sayı doğrusunda göstererek sıralama yapılabilir.
📌 Örnek Problemler
-
Aşağıdaki kesirleri büyükten küçüğe sıralayınız:
13,25,37\frac{1}{3}, \quad \frac{2}{5}, \quad \frac{3}{7}
-
Aşağıdaki ifadelerden hangisi doğrudur?
A) -3/4 > -1/2
B) 2/3 < 3/4
C) 5/8 > 0.75
D) 4/9 = 0.5
Rasyonel Sayılar – 10 Soruluk Test
1. Aşağıdaki ifadelerden hangisi bir rasyonel sayı değildir?
A) 0.5
B) -3/4
C) √2
D) 7/1
2. Aşağıdaki rasyonel sayılardan hangisi sayı doğrusunda 0 ile 1 arasında yer alır?
A) -5/4
B) 3/2
C) 1/3
D) -2/3
3. Aşağıdaki rasyonel sayılardan hangisinin ondalık gösterimi sonlu değildir?
A) 2/5
B) 3/4
C) 7/11
D) 9/10
4. 0.\overline{27} sayısı rasyonel sayı olarak nasıl yazılır?
A) 27/99
B) 3/11
C) 9/50
D) 2/7
5. Aşağıdaki sıralamalardan hangisi doğrudur?
A) 1/2 < 2/3 < 3/4
B) 3/5 < 1/2 < 4/7
C) -5/6 > -1/2
D) 7/8 < 3/4
6. Aşağıdaki işlemlerden hangisinin sonucu en büyüktür?
A) 2/3 + 1/6
B) 5/8 – 1/4
C) 7/9 – 2/3
D) 3/4 × 4/5
7. 0.75 sayısı rasyonel sayı olarak nasıl yazılır?
A) 75/100
B) 3/4
C) 15/20
D) Hepsi doğrudur
8. -3/5 ve -2/7 sayılarından hangisi daha büyüktür?
A) -3/5
B) -2/7
C) İkisi eşittir
D) Karşılaştırılamaz
9. Bir kesrin ondalık gösterimi 1.2\overline{5} şeklinde verilmiştir. Bu sayı hangi rasyonel sayıya eşittir?
A) 125/99
B) 12/5
C) 5/4
D) 15/11
10. Aşağıdaki rasyonel sayılardan hangisi sayı doğrusunda en sağda yer alır?
A) 2/3
B) 3/5
C) 7/8
D) 4/9
Cevap Anahtarı
1 – C
2 – C
3 – C
4 – B
5 – A
6 – D
7 – D
8 – B
9 – D
10 – C

