Dönüşüm Geometrisine Konu Anlatımı

📌 Tanım:
Dönüşüm geometrisi, bir şeklin konumunu değiştirmeden veya belirli kurallar çerçevesinde değiştirerek başka bir noktaya taşınmasını inceleyen geometri dalıdır.

Bu dönüşümler, şeklin büyüklüğünü ve şeklini değiştirmeden farklı bir noktaya taşımasını sağlar. Şeklin boyutu ve açıları korunur, ancak konumu değişir.

🚀 Bu konuda şu dönüşümleri inceleyeceğiz:
✔ Öteleme (Translation): Şeklin belirli bir doğrultuda kaydırılması
✔ Yansıma (Reflection): Şeklin bir eksene göre simetriğinin alınması
✔ Dönme (Rotation): Şeklin bir noktaya göre belirli bir açıda döndürülmesi

Öteleme Hareketi (Translation) Nedir?

📌 Tanım:
Öteleme, bir şeklin boyutunu, şeklini ve yönünü değiştirmeden belirli bir doğrultuda kaydırılmasıdır.

✔ Öteleme sonucunda şeklin tüm noktaları aynı uzaklık ve yönde hareket eder.
✔ Şekil, başlangıç ve bitiş konumunda birebir aynı görünür.
✔ Şeklin açıları ve uzunlukları değişmez, sadece konumu değişir.

🚀 Öteleme işlemi, koordinat sisteminde veya şekiller üzerinde kolayca gösterilebilir.

1. Öteleme Hareketinin Özellikleri

✔ Şeklin büyüklüğü ve yönü değişmez.
✔ Tüm noktalar aynı yönde ve aynı mesafede hareket eder.
✔ Öteleme bir vektör ile ifade edilir.

📌 Öteleme Vektörü:
Bir noktayı veya şekli sağa, sola, yukarı veya aşağı belirli bir miktar kaydıran vektördür.
Örneğin, (x, y) noktası (a, b) kadar ötelenirse yeni noktası:

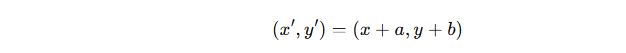
2. Koordinat Düzleminde Öteleme

3. Çokgenlerin Ötelenmesi

📌 Bir çokgenin öteleme hareketi sonucunda:
✔ Kenar uzunlukları değişmez.
✔ Açı ölçüleri değişmez.
✔ Şekil döndürülmez veya yansımaz, sadece kaydırılır.

✅ Örnek:
Bir dikdörtgen (x ekseninde 5 birim sağa, y ekseninde 3 birim yukarı ötelenirse) tüm noktalar aynı şekilde kaydırılır ve yeni konumu belirlenir.

4. Gerçek Hayatta Öteleme Hareketi

✔ Metro Kapıları: Metro kapıları sağa veya sola kayarak açılır ve bu bir öteleme hareketidir.
✔ Asansör Butonları: Kat numaraları yukarı veya aşağı kayarak gösterilir.
✔ Oyunlarda Karakter Hareketleri: Bir oyun karakteri yukarı, aşağı, sağa veya sola hareket ettiğinde öteleme hareketi yapar.

Yansıma Hareketi (Reflection) Nedir?

📌 Tanım:
Yansıma, bir şeklin belirli bir eksene göre simetriğinin alınmasıdır.

✔ Şeklin yönü değişebilir, ancak boyutu ve açılar aynı kalır.
✔ Yansıyan şekil, orijinal şekle göre ters çevrilmiş gibi görünür.
✔ Şekil, yansıma eksenine eşit uzaklıkta bulunur.

🚀 Yansıma hareketi, simetri ve aynadaki görüntüler gibi gerçek dünyada sıkça karşılaşılan bir dönüşümdür.

1. Yansıma Hareketinin Özellikleri

✔ Şeklin boyutu, açısı ve kenar uzunlukları değişmez.
✔ Yalnızca konumu değişir, ters görüntüsü oluşur.
✔ Şekil, yansıma eksenine simetrik olarak yerleştirilir.

📌 Önemli:
Yansıma ekseni, x ekseni, y ekseni veya belirli bir doğru (örneğin y = x) olabilir.

2. Koordinat Düzleminde Yansıma Kuralları

Yansıma işlemi, koordinat sisteminde şu şekilde gösterilir:

3. Çokgenlerin Yansıması

📌 Bir çokgenin yansıması sonucunda:
✔ Tüm noktalar yansıma eksenine eşit uzaklıkta olur.
✔ Şeklin boyutu ve açıları değişmez, ancak yönü değişebilir.
✔ Şekil ters çevrilmiş gibi görünür.

✅ Örnek:
Bir üçgen, x eksenine göre yansıtıldığında, tüm noktalarının y koordinatı işaret değiştirir.

4. Gerçek Hayatta Yansıma Hareketi

✔ Aynadaki Görüntü: Aynaya baktığımızda oluşan görüntü bir yansımadır.
✔ Suya Yansıyan Cisimler: Gölde görülen ağaçlar, yansıma hareketine bir örnektir.
✔ Trafik Levhaları: Bazı levhalar, sürücülerin aynada doğru görmesi için ters yazılır.

Dönme Hareketi (Rotation) Nedir?

📌 Tanım:
Dönme hareketi, bir şeklin belirli bir noktaya göre belli bir açıyla döndürülmesi işlemidir.

✔ Dönme işlemi sonucunda şeklin boyutu, açıları ve kenar uzunlukları değişmez.
✔ Şekil, belirlenen noktaya göre saat yönünde veya saat yönünün tersine döndürülebilir.
✔ Dönme işlemi, genellikle orijin (0,0) noktası etrafında yapılır.

🚀 Bu dönüşüm, rüzgâr türbinleri, çarklar ve pervaneler gibi birçok alanda kullanılır.

1. Dönme Hareketinin Özellikleri

✔ Şeklin boyutu değişmez.
✔ Tüm noktalar, belirlenen dönüş noktasına eşit uzaklıkta kalır.
✔ Saat yönünde veya tersine döndürülebilir.

📌 Önemli:
Dönme işlemi genellikle 90°, 180° ve 270°’lik açılarla yapılır.

2. Koordinat Düzleminde Dönme Kuralları

📌 Orijin (0,0) etrafında döndürme işlemi şu şekilde yapılır:

3. Çokgenlerin Dönmesi

📌 Bir çokgen döndürüldüğünde:
✔ Şeklin büyüklüğü değişmez.
✔ Tüm noktalar, dönme noktasına eşit uzaklıkta hareket eder.
✔ Şeklin yönü değişebilir.

✅ Örnek:
Bir kare, orijin etrafında 90° saat yönünün tersine döndürülürse, tüm köşe noktaları yukarıda belirtilen kurallara göre yer değiştirir.

4. Gerçek Hayatta Dönme Hareketi

✔ Saat Yelkovanı ve Akrebi: Saatin akrep ve yelkovanı belirli açılarla döner.
✔ Rüzgâr Gülleri: Rüzgâr türbinleri, belirli bir eksende döner.
✔ Araba Direksiyonu: Direksiyon çevirildiğinde, tekerlekler belirli bir açıyla döner.

Dönüşüm Geometrisinde Eş ve Benzer Şekiller

Dönüşüm geometrisinde yapılan öteleme, yansıma ve dönme hareketleri, şekillerin eşliğini ve benzerliğini etkileyebilir. Bu dönüşümler sırasında şeklin boyutu ve açıları korunursa şekil eş, sadece boyutu değişirse şekil benzer olur.

1. Dönüşümlerde Eş Şekiller

📌 Tanım:
Bir şekil yalnızca konumunu veya yönünü değiştirirse ve boyutu aynı kalırsa, şekil eş kalır.

✔ Öteleme, yansıma ve dönme hareketlerinde şekiller her zaman eş şekiller oluşturur.
✔ Eş şekillerin tüm kenar uzunlukları ve açıları aynıdır.
✔ Eşlik “≅” sembolü ile gösterilir.

✅ Örnek:
Bir kare orijin etrafında 180° döndürülürse, yeni konumu farklı olsa da şekil aynıdır.

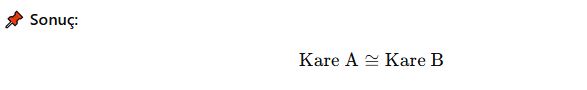
Bu iki kare eş şekillerdir çünkü büyüklükleri değişmemiştir.

2. Dönüşümlerde Benzer Şekiller

📌 Tanım:
Eğer dönüşüm sırasında bir şeklin boyutu değişirse (büyütme veya küçültme yapılırsa), ancak açıları ve şekli korunursa, bu şekiller benzer olur.

✔ Benzer şekillerin açıları aynıdır, ancak kenar uzunlukları belirli bir oranla büyür veya küçülür.
✔ Benzerlik oranı kullanılarak şeklin boyutu belirlenir.
✔ Benzerlik “∼” sembolü ile gösterilir.

✅ Örnek:
Bir üçgenin tüm kenarları 2 katına çıkarılırsa, şeklin açılarında bir değişiklik olmaz, ancak kenarları büyüdüğü için yeni şekil orijinal üçgene benzer olur.

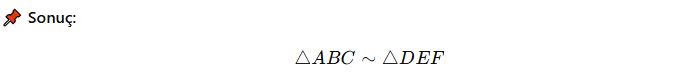
Bu üçgenler benzer şekillerdir çünkü açıları aynıdır, ancak kenar uzunlukları farklı bir oranda büyütülmüştür.

3. Hangi Dönüşümler Eşlik ve Benzerlik Oluşturur?

📌 Özetle:
✔ Öteleme, yansıma ve dönme hareketleri sonucunda şekiller eş kalır.
✔ Büyütme veya küçültme hareketi sonucunda şekiller benzer olur.

4. Gerçek Hayatta Dönüşüm Geometrisi ile Eş ve Benzer Şekiller

✔ Oyun Karakterlerinin Hareketi: Oyunlarda karakterler sağa, sola kayarak veya dönerek hareket eder. Bu hareketler eş şekiller oluşturur.
✔ Aynadaki Görüntüler: Aynadaki yansıma, şeklin eş hâlidir.
✔ Projeksiyon Cihazları: Görüntüyü büyütüp küçültme işlemi, benzer şekiller oluşturur.
✔ Harita Ölçekleri: Küçültülmüş haritalar, gerçek bölgenin benzeridir.

📌 Bu konuda öğrendiklerimiz:
✅ Öteleme, yansıma ve dönme hareketlerinin eş şekiller oluşturduğunu öğrendik.
✅ Büyütme veya küçültme işlemlerinin benzer şekiller oluşturduğunu gördük.
✅ Dönüşüm geometrisinde eş ve benzer şekillerin nasıl oluştuğunu inceledik.
✅ Gerçek hayatta dönüşüm geometrisinin kullanım alanlarını öğrendik.

Dönüşüm Geometrisi Konu Özeti

Bu konu boyunca öteleme, yansıma ve dönme hareketlerini, dönüşümlerde eş ve benzer şekillerin nasıl oluştuğunu öğrendik. İşte öğrendiklerimizin kısa bir özeti:

1. Öteleme (Translation) Nedir?

📌 Tanım:
Öteleme, bir şeklin boyutunu ve yönünü değiştirmeden belirli bir doğrultuda kaydırılmasıdır.

✔ Şekil aynı kalır, sadece konumu değişir.
✔ Tüm noktalar aynı yönde ve aynı mesafede hareket eder.
✔ Öteleme işlemi bir vektör ile ifade edilir.

📌 Koordinat sisteminde öteleme kuralları:

2. Yansıma (Reflection) Nedir?

📌 Tanım:
Yansıma, bir şeklin belirli bir eksene göre simetriğinin alınmasıdır.

✔ Şeklin yönü değişebilir, ancak boyutu ve açılar aynıdır.
✔ Şekil, yansıma eksenine eşit uzaklıkta olur.

📌 Koordinat sisteminde yansıma kuralları:

3. Dönme (Rotation) Nedir?

📌 Tanım:
Dönme hareketi, bir şeklin belirli bir noktaya göre belli bir açıyla döndürülmesidir.

✔ Şeklin boyutu ve açıları değişmez, sadece yönü değişir.
✔ Saat yönünde veya saat yönünün tersine dönebilir.

📌 Orijin etrafında dönme kuralları:

4. Dönüşümlerde Eş ve Benzer Şekiller

📌 Eşlik:
✔ Öteleme, yansıma ve dönme hareketleri sonucunda şekiller her zaman eş şekiller oluşturur.
✔ Şeklin boyutu, açılar ve kenar uzunlukları değişmez.
✔ Eşlik “≅” sembolü ile gösterilir.

📌 Benzerlik:
✔ Bir şeklin büyütülmesi veya küçültülmesiyle oluşan şekiller benzer olur.
✔ Benzerlik “∼” sembolü ile gösterilir.

✅ Örnek:
Bir üçgen 2 kat büyütülürse, yeni şekil benzer olur ancak eş olmaz.

5. Gerçek Hayatta Dönüşüm Geometrisi

✔ Oyun Karakterlerinin Hareketi: Oyunlarda karakterler sağa, sola kayarak veya dönerek hareket eder.
✔ Aynadaki Görüntüler: Aynadaki yansıma, şeklin eş hâlidir.
✔ Rüzgâr Gülleri: Rüzgâr türbinleri belirli bir eksende döner.
✔ Projeksiyon Cihazları: Görüntüyü büyütüp küçültme işlemi, benzer şekiller oluşturur.

📌 Bu konu kapsamında öğrendiklerimiz:
✅ Öteleme, yansıma ve dönme hareketlerinin nasıl yapıldığını öğrendik.
✅ Koordinat sisteminde bu dönüşümlerin nasıl uygulandığını gördük.
✅ Dönüşümlerde hangi şekillerin eş, hangi şekillerin benzer olduğunu öğrendik.
✅ Gerçek hayatta dönüşüm geometrisinin kullanım alanlarını inceledik.

8. Sınıf Matematik Dönüşüm Geometrisi Çözümlü Örnek Sorular

1. Öteleme Hareketi

📌 Soru 1:
A(2, 3) noktası 5 birim sağa ve 4 birim aşağı ötelenirse yeni koordinatları ne olur?

2. Yansıma Hareketi (x Eksenine Göre Yansıma)

📌 Soru 2:
B(4, -6) noktası x eksenine göre yansıtıldığında yeni koordinatları ne olur?

3. Yansıma Hareketi (y Eksenine Göre Yansıma)

📌 Soru 3:
C(-3, 7) noktası y eksenine göre yansıtıldığında yeni koordinatları ne olur?

4. Dönme Hareketi (Orijin Etrafında 90° Dönme)

📌 Soru 4:
D(5, 2) noktası orijin etrafında 90° saat yönünün tersine döndürülürse yeni koordinatları ne olur?

5. Dönme Hareketi (Orijin Etrafında 180° Dönme)

📌 Soru 5:
E(-4, -7) noktası orijin etrafında 180° döndürülürse yeni koordinatları ne olur?

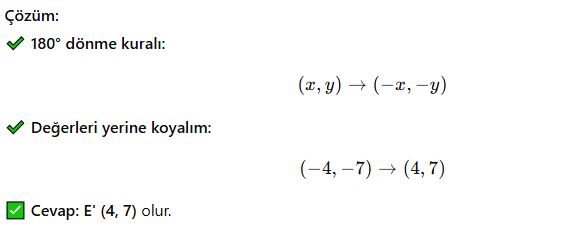
6. Öteleme Hareketi (Koordinat Sistemi Üzerinde)

📌 Soru 6:
F(–2, 5) noktası x ekseninde 6 birim sağa, y ekseninde 3 birim yukarı ötelenirse yeni koordinatları ne olur?

7. Yansıma Hareketi (y = x Doğrusuna Göre Yansıma)

📌 Soru 7:
G(6, -2) noktası y = x doğrusuna göre yansıtılırsa yeni koordinatları ne olur?

8. Yansıma Hareketi (y = -x Doğrusuna Göre Yansıma)

📌 Soru 8:
H(-3, 7) noktası y = -x doğrusuna göre yansıtılırsa yeni koordinatları ne olur?

9. Dönme Hareketi (Orijin Etrafında 270° Dönme)

📌 Soru 9:
I(1, 4) noktası orijin etrafında 270° saat yönünün tersine döndürülürse yeni koordinatları ne olur?

10. Şekil Üzerinde Yansıma ve Dönme

📌 Soru 10:
Bir üçgenin köşe noktaları A(1,2), B(3,4) ve C(5,6) olarak verilmiştir. Bu üçgen x eksenine göre yansıtılırsa yeni köşe noktaları ne olur?

📌 Bu 10 soru ile şunları öğrendik:
✔ Öteleme işlemiyle koordinat noktalarını kaydırmayı öğrendik.
✔ x ve y eksenine göre yansıma kurallarını uyguladık.
✔ y = x ve y = -x doğrularına göre yansıtma yaptık.
✔ Orijin etrafında 90°, 180° ve 270° dönüşlerin nasıl yapıldığını gördük.
✔ Şekillerin köşe noktalarını yansıtma v döndürme kurallarına göre hesapladık.