Günlük hayatımızda anketler, sınav sonuçları, hava durumu tahminleri, istatistikler gibi birçok veriye rastlarız. Bu verilerin anlamlı hale getirilmesi ve yorumlanması için veri analizi yöntemleri kullanılır. Veri analizi, bilgiyi düzenleyerek, özetleyerek ve yorumlayarak daha sağlıklı kararlar almamıza yardımcı olur.

8. Sınıf Matematik Veri Analizi Konu Anlatımı

Bu konu kapsamında veri toplama, sıklık tabloları, merkezi eğilim ölçüleri (ortalama, medyan, mod), dağılım ölçüleri (standart sapma, açıklık) ve veri yorumlama yöntemleri gibi önemli başlıkları inceleyeceğiz. İlk olarak “Veri Toplama ve Sınıflandırma” konusuna giriş yapalım. 🚀

Veri Toplama ve Sınıflandırma

Veri analizi yapabilmek için önce verileri toplamak, düzenlemek ve sınıflandırmak gerekir. Veri toplama sürecinde doğru, güvenilir ve amaca uygun veriler seçilmelidir. Bu veriler daha sonra tablolar ve grafikler yardımıyla sınıflandırılır ve analiz edilir.

1. Veri Nedir?

📌 Tanım:
Veri, bir olay, durum veya araştırma hakkında toplanan sayısal veya sözel bilgilerdir.

📌 Örnekler:

• Sınıftaki öğrencilerin yaşları: 12, 13, 12, 14, 13, 12
• Bir mağazadaki günlük satış miktarları: 45, 50, 48, 52, 47
• Sınav notları: 80, 90, 75, 85, 95

Veriler düzenli hale getirilerek anlamlı bilgiler çıkarılır.

2. Veri Türleri

Veriler nicel (sayısal) ve nitel (niteliksel) olmak üzere ikiye ayrılır.

a) Nicel (Sayısal) Veriler

📌 Tanım: Sayılarla ifade edilebilen verilerdir.

✅ Örnekler:

• Bir öğrencinin boyu: 160 cm
• Bir sınıftaki öğrenci sayısı: 30 kişi
• Günlük hava sıcaklıkları: 22°C, 25°C, 18°C

📌 İki Türü Vardır:

• Sürekli veri: Ölçülebilen değerler (Boy uzunluğu, ağırlık, sıcaklık).
• Kesikli veri: Sayılabilen değerler (Öğrenci sayısı, araba sayısı, ev sayısı).

b) Nitel (Niteliksel) Veriler

📌 Tanım: Sayılarla ifade edilemeyen, özellikleri belirten verilerdir.

✅ Örnekler:

• Göz rengi: Mavi, kahverengi, yeşil
• Sevilen ders: Matematik, Türkçe, Fen Bilimleri
• Kişinin memnuniyeti: Mutlu, orta, mutsuz

📌 Not: Nitel veriler kategori şeklinde gösterilir ve grafikler yardımıyla analiz edilir.

3. Veri Toplama Yöntemleri

Veri analizi yaparken verinin nasıl toplandığı çok önemlidir. Yanlış veri toplama, hatalı sonuçlara yol açabilir.

📌 Veri toplama yöntemleri şunlardır:

✅ Örnek:
Bir okulda öğrencilerin en sevdiği spor dalını belirlemek için anket uygulanır. Anket sonuçları grafik ve tablo ile gösterilir.

4. Sınıflandırma ve Sıklık Tablosu Oluşturma

Verileri düzenli bir hale getirmek için sıklık tablosu kullanılır.

📌 Sıklık Tablosu:
Bir veri kümesinde her bir değerin kaç kez tekrarlandığını gösteren tablodur.

✅ Örnek:
Bir sınıfta öğrencilerin en sevdiği renkler şu şekilde olsun:
Mavi, Kırmızı, Mavi, Yeşil, Kırmızı, Mavi, Sarı, Kırmızı, Yeşil, Mavi

Bu verileri sıklık tablosunda gösterelim:

📌 Sonuç: En sevilen renk Mavi olmuştur.

5. Grafiklerle Gösterim

Veriler grafiklerle gösterildiğinde daha kolay analiz edilir. En yaygın kullanılan grafik türleri:

1️⃣ Çubuk Grafiği: Sayısal verileri karşılaştırmak için kullanılır.
2️⃣ Daire Grafiği: Bir bütünün parçalarını göstermek için kullanılır.
3️⃣ Sütun Grafiği: Kategorik verileri karşılaştırmak için kullanılır.

✅ Örnek:
Bir okulda öğrencilerin favori dersleri aşağıdaki gibidir:

• Matematik: 8 kişi
• Fen: 6 kişi
• Türkçe: 5 kişi
• Sosyal Bilgiler: 4 kişi

Bu verileri çubuk grafiği ile gösterelim:

📊 Grafik:
Matematik ██████████ (8)
Fen ████████ (6)
Türkçe ██████ (5)
Sosyal Bilgiler ████ (4)

📌 Sonuç: En sevilen ders Matematik olmuştur.

6. Gerçek Hayatta Kullanımı

📌 Örnekler:

• İklim Bilimleri: Hava sıcaklıklarını analiz ederek tahminler yapılır.
• Ekonomi: Enflasyon oranları, fiyat değişimleri analiz edilir.
• Sağlık: Hasta verileri analiz edilerek hastalık yayılımı tespit edilir.
• Spor: Takımların istatistikleri değerlendirilerek analiz yapılır.

✅ Örnek:
Bir mağaza, satışlarını artırmak için müşteri tercihlerini analiz eder. En çok satılan ürünlerin verileri kullanılarak stok yönetimi yapılır.

📌 Bu konuda öğrendiklerimiz:
✅ Veri türlerini (nicel/nitel) öğrendik.
✅ Veri toplama yöntemlerini inceledik.
✅ Sıklık tabloları ve grafiklerle verileri nasıl gösterileceğini öğrendik.
✅ Gerçek hayatta veri analizinin nasıl kullanıldığını gördük.

Merkezi Eğilim Ölçüleri (Ortalama, Medyan, Mod)

Bir veri grubundaki temel eğilimleri belirlemek için merkezi eğilim ölçüleri kullanılır. Bunlar:

• Aritmetik Ortalama (Ort): Verilerin toplamının veri sayısına bölünmesiyle bulunur.
• Medyan (Ortanca): Verilerin küçükten büyüğe sıralandığında ortada kalan değeridir.
• Mod (Tepe Değer): Veri setinde en çok tekrar eden değerdir.

Bu ölçüler, veri setini özetlemek ve anlamlandırmak için kullanılır.

1. Aritmetik Ortalama (Ort)

📌 Tanım:
Bir veri grubundaki tüm sayıların toplamının, veri sayısına bölünmesiyle bulunur.

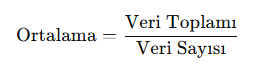
✅ Örnek:
Bir öğrencinin son 5 sınav notu: 80, 85, 90, 95, 100

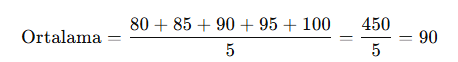
✅ Sonuç: Ortalama = 90

📌 Özellikler:
✔ Aritmetik ortalama, verilerin tamamını dikkate alır.
✔ Aykırı değerler (çok büyük veya çok küçük sayılar) ortalamayı etkileyebilir!

✅ Örnek:
4, 5, 6, 7, 100 için ortalama:

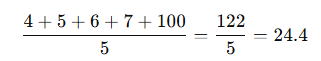
Burada 100 çok büyük bir değer olduğu için ortalamayı yükseltmiştir.

2. Medyan (Ortanca)

📌 Tanım:
Bir veri grubundaki sayılar küçükten büyüğe sıralandığında ortada kalan değer medyandır.

✅ Örnek 1 (Tek Sayıda Veri Seti):
Veri seti: 10, 20, 30, 40, 50

• Ortadaki sayı = 30 ✅

✅ Örnek 2 (Çift Sayıda Veri Seti):
Veri seti: 10, 20, 30, 40, 50, 60

• Ortada iki sayı var: 30 ve 40
• Medyan = (30 + 40) ÷ 2 = 35 ✅

📌 Özellikler:
✔ Medyan, aykırı değerlerden etkilenmez.
✔ Veriler küçükten büyüğe sıralanmalıdır!

✅ Örnek:
Sayılar 1, 2, 3, 100, 150 olsun.

• Ortalama = (1+2+3+100+150) ÷ 5 = 51.2
• Medyan = 3 (Ortadaki sayı)

Burada 100 ve 150 aykırı değer olduğu için ortalama yükselmiş, ancak medyan etkilenmemiştir.

3. Mod (Tepe Değer)

📌 Tanım:
Bir veri grubunda en çok tekrar eden değer mod (tepe değer) olarak adlandırılır.

✅ Örnek 1:
Veri seti: 2, 3, 3, 5, 6, 3, 7, 8

• Mod = 3 (Çünkü en çok tekrar eden sayı 3’tür) ✅

✅ Örnek 2 (Mod Olmayan Durum):
Veri seti: 2, 4, 6, 8, 10

• Her sayı sadece bir kez geçtiği için mod yoktur. ❌

✅ Örnek 3 (Birden Fazla Mod):
Veri seti: 1, 2, 2, 3, 3, 4

• Hem 2 hem de 3 en çok tekrar eden değerlerdir.
• Mod = 2 ve 3 (Çok Modlu Veri Seti) ✅

📌 Özellikler:
✔ Mod, en çok tekrar eden değeri gösterir.
✔ Mod, kesin bir merkezi eğilim ölçüsü değildir, bazı veri setlerinde mod olmayabilir.

4. Aritmetik Ortalama, Medyan ve Mod Arasındaki Farklar

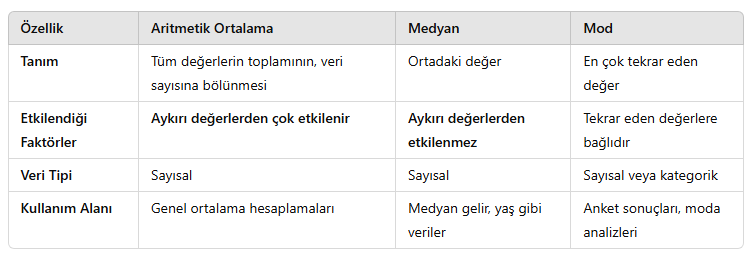
5. Gerçek Hayatta Kullanımı

📌 Örnek Kullanım Alanları:

✔ Aritmetik Ortalama:

• Sınav sonuçlarının değerlendirilmesi
• Ülke genelinde maaş ortalaması hesaplama

✔ Medyan:

• Gelir dağılımı analizi (Aykırı değerler olabileceği için medyan daha güvenilirdir.)
• Emlak fiyatları hesaplamalarında

✔ Mod:

• Anket sonuçları (En çok tercih edilen marka, favori renk vb.)
• Moda sektöründe en popüler renk veya model belirleme

✅ Örnek:
Bir şirketin çalışan maaşları: 3.000 TL, 3.500 TL, 4.000 TL, 25.000 TL

• Ortalama = (3.000 + 3.500 + 4.000 + 25.000) ÷ 4 = 8.875 TL
• Medyan = (3.500 + 4.000) ÷ 2 = 3.750 TL
• Mod = Yok (Tekrar eden değer yoktur.)

📌 Sonuç:
Aşırı yüksek maaş ortalamanın çok yükselmesine sebep olduğu için, medyan daha iyi bir ölçüdür.

📌 Bu konuda öğrendiklerimiz:
✅ Aritmetik ortalama nasıl hesaplanır?
✅ Medyan nasıl bulunur ve neden kullanılır?
✅ Mod nasıl hesaplanır ve neyi ifade eder?
✅ Bu üç merkezi eğilim ölçüsünün farklarını gördük.

Veri Gruplarında Dağılım Ölçüleri (Açıklık ve Standart Sapma)

Merkezi eğilim ölçüleri (ortalama, medyan, mod) verilerin genel eğilimini gösterirken, dağılım ölçüleri ise verilerin ne kadar yayılmış olduğunu gösterir.

Bu bölümde açıklık ve standart sapma kavramlarını inceleyeceğiz.

1. Açıklık (Ranj) Nedir?

📌 Tanım:
Açıklık, veri setindeki en büyük değerden en küçük değerin çıkarılmasıyla elde edilir.

✅ Örnek:
Bir sınıftaki öğrencilerin sınav notları: 50, 60, 70, 80, 90

✅ Sonuç: Açıklık = 40

📌 Özellikler:
✔ Açıklık, veri setinin genişliğini gösterir.
✔ Aykırı değerlerden çok etkilenir (çok büyük veya küçük değerler açıklığı artırır).

✅ Örnek:

• Sınav notları: 10, 20, 30, 40, 90
• Açıklık: 90 – 10 = 80 (Çünkü 90 çok büyük bir değer)

📌 Sonuç:
Bu veri setinde 90 gibi büyük bir değer olduğu için açıklık fazla çıkmıştır.

2. Standart Sapma Nedir?

📌 Tanım:
Standart sapma, verilerin ortalamadan ne kadar uzaklaştığını gösteren bir ölçüdür.

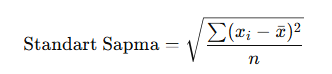
Burada:

• xix_ixi​ → Veriler
• xˉ\bar{x}xˉ → Aritmetik Ortalama
• $n$ → Veri Sayısı

✅ Örnek:
İki sınıfta yapılan sınav sonuçları:

1. Sınıf: 45, 50, 55, 60, 65
2. Sınıf: 10, 30, 50, 70, 90

İki sınıfın da ortalaması aynıdır (55). Ancak:

• 1. Sınıfta öğrencilerin notları ortalamaya yakın → Standart sapma düşük
• 2. Sınıfta notlar çok farklı → Standart sapma yüksek

📌 Sonuç:
✔ Standart sapma küçükse → Veriler ortalamaya yakındır, çok fazla farklılık yoktur.
✔ Standart sapma büyükse → Veriler çok dağınıktır, değişkenlik fazladır.

✅ Örnek:

• Notlar: 40, 50, 60 → Standart Sapma Küçük
• Notlar: 10, 50, 90 → Standart Sapma Büyük

3. Açıklık ve Standart Sapma Arasındaki Farklar

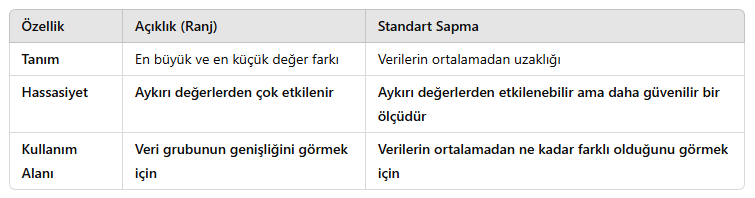
4. Gerçek Hayatta Kullanımı

📌 Örnek Kullanım Alanları:

✔ Açıklık:

• Bir mağazadaki en yüksek ve en düşük satışları analiz etmek
• Sınavlardaki en yüksek ve en düşük not farkını incelemek

✔ Standart Sapma:

• Öğrencilerin sınav sonuçlarının birbirine yakın olup olmadığını anlamak
• Hisse senedi fiyatlarının ne kadar dalgalandığını analiz etmek

✅ Örnek:
İki markette satılan süt fiyatları inceleniyor:

• Market A: Fiyatlar birbirine yakın (standart sapma düşük)
• Market B: Fiyatlar çok değişken (standart sapma yüksek)

📌 Sonuç:
Market B’de süt fiyatları daha dengesiz, Market A’da daha sabittir.

📌 Bu konuda öğrendiklerimiz:
✅ Açıklık nasıl hesaplanır ve neyi gösterir?
✅ Standart sapma nedir ve neden önemlidir?
✅ Gerçek hayatta açıklık ve standart sapmanın nasıl kullanıldığını gördük.

Veri Yorumlama

Veri analizi yapıldıktan sonra çıkan sonuçların yorumlanması, bilgiyi doğru anlamamızı sağlar. Veri yorumlama sürecinde, grafikler, tablolar, merkezi eğilim ölçüleri ve dağılım ölçüleri kullanılır.

Bu bölümde, veri setlerinden nasıl anlamlı sonuçlar çıkarabileceğimizi detaylı olarak inceleyeceğiz.

1. Verileri Grafik ve Tablolarla Yorumlama

Verileri daha iyi anlayabilmek için grafikler ve tablolar kullanılır. En sık kullanılan grafik türleri:

📌 Çubuk Grafiği → Kategorik verileri karşılaştırmak için kullanılır.
📌 Daire Grafiği → Bir bütünün parçalarını yüzdelik olarak göstermek için kullanılır.
📌 Sütun Grafiği → Sayısal verileri görselleştirmek için kullanılır.

✅ Örnek:
Bir anket çalışmasında öğrencilerin favori spor dalları belirlenmiştir:

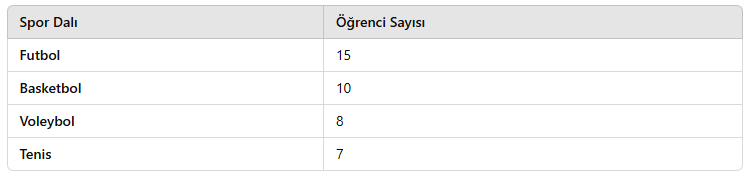
📊 Çubuk Grafiği İle Yorum:

• Futbol, en çok tercih edilen spor dalıdır.
• Tenis, en az tercih edilen spordur.
• Futbol ve basketbol arasında büyük bir fark vardır.

📌 Sonuç: Öğrencilerin çoğunluğu futbolu tercih etmektedir.

2. Merkezi Eğilim Ölçüleriyle Yorumlama

Ortalama, medyan ve mod kullanılarak veri setindeki eğilimler anlaşılabilir.

✅ Örnek:
Bir sınıftaki sınav notları: 50, 55, 60, 65, 100

• Ortalama = 66
• Medyan = 60
• Mod = Yok
• Açıklık = 100 – 50 = 50

📌 Yorum:

• Ortalama yüksektir, ancak 100 puanlık bir aykırı değer bulunmaktadır.
• Medyan, ortalamaya göre daha düşük olup gerçekçi bir ölçümdür.
• Mod olmadığı için en çok tekrar eden bir değer yoktur.

📌 Sonuç: Aykırı değerlerden dolayı ortalama yanıltıcı olabilir, bu nedenle medyan daha güvenilir bir ölçümdür.

3. Dağılım Ölçüleriyle Yorumlama

Standart sapma ve açıklık, verilerin nasıl dağıldığını anlamamıza yardımcı olur.

✅ Örnek:
İki sınıftaki sınav sonuçları:

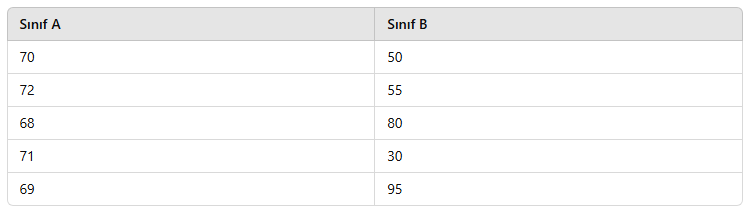
📌 Analiz:

• Sınıf A’nın standart sapması düşük, çünkü notlar birbirine yakındır.
• Sınıf B’nin standart sapması yüksek, çünkü notlar arasında büyük farklar vardır.
• Sınıf A’da notlar daha dengeli, Sınıf B’de ise öğrenciler arasında büyük farklar vardır.

📌 Sonuç:
✔ Sınıf A’da öğrencilerin başarı düzeyi daha istikrarlıdır.
✔ Sınıf B’de başarı durumu çok değişkendir, bazı öğrenciler çok başarılı, bazıları çok düşük not almıştır.

4. Gerçek Hayatta Kullanımı

📌 Örnek Kullanım Alanları:

✔ Eğitim: Öğrencilerin sınav başarılarının analiz edilmesi.
✔ Ekonomi: Gelir dağılımının incelenmesi.
✔ Spor: Takımların performanslarının değerlendirilmesi.
✔ Sağlık: Hastalık oranlarının analiz edilmesi.

✅ Örnek:
Bir şirket, çalışanlarının maaşlarını analiz ederek yeni maaş düzenlemesi yapacaktır.

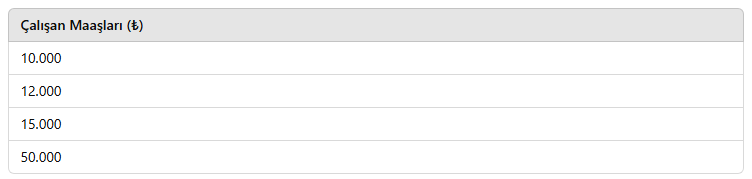
📌 Yorum:
✔ Ortalama maaş yüksek görünse de (yaklaşık 21.750₺), en yüksek maaş aykırı bir değerdir.
✔ Medyan (13.500₺) çalışanların maaşlarını daha doğru yansıtmaktadır.

📌 Sonuç:
✔ Maaş düzenlemesi yapılırken ortalama değil, medyan dikkate alınmalıdır.

📌 Bu konuda öğrendiklerimiz:
✅ Verileri grafik ve tablolarla nasıl yorumlayacağımızı öğrendik.
✅ Merkezi eğilim ve dağılım ölçüleri kullanarak analiz yaptık.
✅ Gerçek hayattaki veri yorumlama örneklerini inceledik.

8. Sınıf Matematik Veri Analizi Örnek Sorular

1. Aritmetik Ortalama Hesaplama

📌 Soru 1:
Bir öğrencinin son 5 sınavdan aldığı notlar: 70, 80, 75, 85, 90
Bu öğrencinin sınav notlarının aritmetik ortalaması nedir?

Çözüm:

✅ Cevap: 80

2. Medyan Bulma

📌 Soru 2:
Bir sınıftaki 7 öğrencinin boy uzunlukları (cm): 150, 155, 160, 162, 165, 170, 175
Bu veri grubunun medyanı (ortanca değeri) kaçtır?

Çözüm:

• Veri küçükten büyüğe sıralanmıştır.
• Ortadaki değer: 162 cm

✅ Cevap: 162 cm

3. Mod (Tepe Değer) Hesaplama

📌 Soru 3:
Bir mağazada satılan ayakkabı numaraları: 38, 40, 42, 38, 39, 40, 38, 41, 40, 40
Bu veri grubunun modu nedir?

Çözüm:

• 38 → 3 kez tekrar ediyor.
• 40 → 4 kez tekrar ediyor.
• Diğer sayılar daha az tekrar ediyor.
• En çok tekrar eden sayı: 40

✅ Cevap: 40

4. Açıklık (Ranj) Hesaplama

📌 Soru 4:
Bir sınıftaki öğrencilerin sınav notları: 45, 50, 65, 70, 80, 85
Bu veri setinin açıklığını (ranjını) bulunuz.

Çözüm:

✅ Cevap: 40

5. Standart Sapmanın Yorumu

📌 Soru 5:
İki farklı sınıfta öğrencilerin sınav notları şu şekildedir:

Sınıf A: 65, 67, 70, 72, 74
Sınıf B: 40, 55, 70, 85, 100

Hangi sınıfta standart sapma daha yüksektir?

Çözüm:

• Sınıf A’daki notlar birbirine çok yakın, standart sapma küçük olur.
• Sınıf B’de notlar çok farklı (40 ve 100 gibi uç noktalar var), standart sapma büyük olur.

✅ Cevap: Sınıf B’de standart sapma daha yüksektir.

6. Grafik Yorumu

📌 Soru 6:
Aşağıdaki çubuk grafiği bir okulda öğrencilerin en sevdiği dersleri göstermektedir:

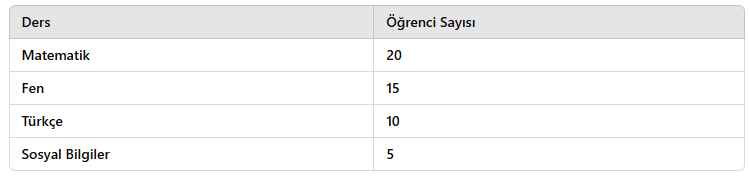
Bu veriye göre aşağıdakilerden hangisi yanlıştır?

A) Matematik en çok sevilen derstir.
B) En az tercih edilen ders Sosyal Bilgiler’dir.
C) Fen ve Türkçe’yi seven öğrenci sayısı eşittir.
D) Matematik ve Fen’i sevenlerin toplamı 35’tir.

Çözüm:

• Matematik en çok tercih edilen ders → Doğru ✅
• Sosyal Bilgiler en az tercih edilen ders → Doğru ✅
• Fen = 15, Türkçe = 10 → Farklı olduğu için yanlış ❌
• Matematik (20) + Fen (15) = 35 → Doğru ✅

✅ Cevap: C) Fen ve Türkçe’yi seven öğrenci sayısı eşittir. (Yanlış)

7. Aritmetik Ortalama ile Medyan Karşılaştırması

📌 Soru 7:
Bir sınıftaki öğrencilerin sınav notları: 40, 50, 60, 70, 100
Bu veri kümesi için aritmetik ortalama mı yoksa medyan mı daha iyi bir ölçüdür?

Çözüm:

• Ortalama:

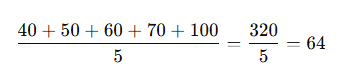
• Medyan:
  • Sıralanmış veride ortadaki değer → 60

📌 Yorum:

• Aykırı değer (100) ortalamayı yükseltmiştir.
• Medyan aykırı değerlerden etkilenmez, bu yüzden daha güvenilir bir ölçüdür. ✅

✅ Cevap: Medyan daha iyi bir ölçüdür.

8. Modu Olmayan Veri Kümesi

📌 Soru 8:
Aşağıdaki veri kümesi için mod (tepe değer) var mıdır?

Veri Seti: 3, 5, 7, 9, 11

Çözüm:

• Her sayı yalnızca bir kez geçtiği için tepe değer (mod) yoktur. ❌

✅ Cevap: Mod yoktur.

9. Açıklık ve Standart Sapma Karşılaştırması

📌 Soru 9:
İki mağazada satılan ayakkabı fiyatları aşağıdaki gibidir:

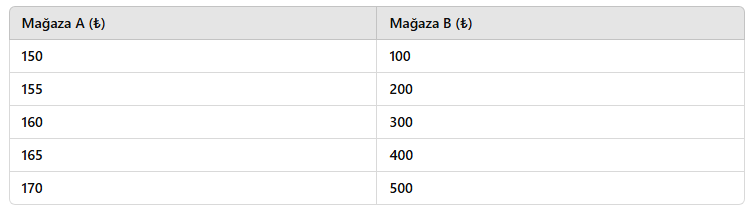
Hangi mağazada fiyat değişkenliği daha fazladır?

Çözüm:

• Açıklık (Ranj):
  • Mağaza A: 170 – 150 = 20
  • Mağaza B: 500 – 100 = 400

📌 Yorum:

• Mağaza A’da fiyatlar birbirine yakın, Mağaza B’de ise çok değişken.
• Mağaza B’nin açıklığı çok büyük olduğu için değişkenlik fazla.

✅ Cevap: Mağaza B’de fiyat değişkenliği daha fazladır.

10. Gerçek Hayatta Veri Yorumu

📌 Soru 10:
Bir şehirdeki hava sıcaklıkları aşağıdaki gibidir:

Şehir A: 20°C, 21°C, 19°C, 22°C, 21°C
Şehir B: 10°C, 25°C, 30°C, 5°C, 20°C

Hangi şehirde sıcaklıklar daha stabildir?

Çözüm:

• Şehir A’da sıcaklıklar birbirine çok yakın, değişkenlik azdır.
• Şehir B’de sıcaklıklar çok farklı (5°C ve 30°C gibi uç değerler var), değişkenlik fazladır.

✅ Cevap: Şehir A’da sıcaklıklar daha stabildir.

📌 10 soru boyunca şunları öğrendik:
✔ Aritmetik ortalama, medyan ve mod hesaplamalarını yaptık.
✔ Açıklık ve standart sapmayı yorumladık.
✔ Gerçek hayatta veri analizinin nasıl yapıldığını gördük.