AYT Matematik Sayı Basamakları Konu Anlatımı

Matematikte sayı sistemlerini anlamanın en temel adımlarından biri sayı basamakları konusudur. Bir sayıyı oluşturan rakamların konumlarının farklı değerler ifade ettiğini öğrenmek, işlemlerin doğruluğunu artırır ve ileri düzey problemlerde pratiklik sağlar. AYT seviyesinde bu konu, özellikle çözümleme, taban sistemleri ve basamak değerleri ile ilgili ileri seviye sorular içerebilir.

Bir sayıyı basamaklarına ayırarak çözümlemek, özellikle modüler aritmetik, sayı sistemleri ve dijital kök hesaplamalarında sıkça kullanılır. Ayrıca, taban aritmetiği ve farklı sayı sistemleriyle ilgili işlemleri anlayabilmek için bu konulara hâkim olmak önemlidir.

Bu ünitede ele alacağımız konular şunlardır:

1. Sayı Basamağı – Sayının basamakları ve basamak değeri kavramları
2. Çözümleme – Sayıların genişletilmiş formda yazılması
3. Taban – Farklı taban sistemlerinde sayı gösterimleri

Şimdi, bu alt başlıkları tek tek ele alarak derinlemesine incelemeye başlayalım. 🚀

Sayı Basamağı ve Basamak Değeri

Sayı basamağı, bir sayıyı oluşturan rakamların konumlarına göre taşıdığı değeri ifade eden yapıdır. Her rakamın bulunduğu basamağa göre farklı bir değeri vardır.

Örneğin, 4.523 sayısında:

• 4, binler basamağında (4.000)
• 5, yüzler basamağında (500)
• 2, onlar basamağında (20)
• 3, birler basamağında (3)

Bu şekilde her rakamın bulunduğu basamağa göre değeri değişir.

Basamak Değeri Nedir?

Bir sayının herhangi bir basamağında bulunan rakamın, o basamağın değeri ile çarpılmasıyla elde edilen değere basamak değeri denir.

Örneğin:

Özel Durumlar:

• Bir basamaktaki rakam 0 ise, o basamağın değeri de 0 olur.
  Örneğin, 2.073 sayısında yüzler basamağında 0 olduğu için basamak değeri 0’dır.
• Bir sayının en sağındaki basamak birler basamağıdır ve değeri rakamın kendisidir.
  Örneğin, 347 sayısında 7’nin basamak değeri = 7’dir.

Örnek Soru:

Aşağıdaki sayılardan hangisinin yüzler basamağındaki rakamın basamak değeri 600’dür?
A) 6.432
B) 7.654
C) 8.625
D) 9.607

Çözüm:
Yüzler basamağı, en sağdan üçüncü basamaktır. 600 değeri alabilmesi için yüzler basamağındaki rakam 6 olmalıdır.

• A şıkkı: 6.432 → Yüzler basamağı 4 → Basamak değeri 400 ❌
• B şıkkı: 7.654 → Yüzler basamağı 6 → Basamak değeri 600 ✅
• C şıkkı: 8.625 → Yüzler basamağı 6 → Basamak değeri 600 ✅
• D şıkkı: 9.607 → Yüzler basamağı 6 → Basamak değeri 600 ✅

Doğru cevap: B, C ve D şıklarıdır. ✅

Çözümleme

Bir sayının her basamağındaki rakamın basamak değeriyle ifade edilerek genişletilmiş formda yazılmasına çözümleme denir.

Örnek:

Bu yöntemi kullanarak sayıları analiz etmek, işlemleri daha kolay hale getirebilir.

Genel formül:

Örneğin:

• 7.345 sayısını çözümleyelim:
  

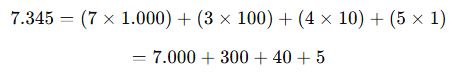
Bu yöntem, özellikle farklı tabanlarda sayı yazılımlarında da önemlidir.

Örnek Soru:

6.702 sayısının çözümleme işlemi aşağıdakilerden hangisidir?
A) 6.000 + 700 + 2
B) 6.000 + 7.000 + 2
C) 6.000 + 70 + 2
D) 60 + 700 + 2

Çözüm:

6.702=6.000+700+2

Doğru cevap: A ✅

Taban Aritmetiği (Farklı Sayı Sistemleri)

Günlük hayatta kullandığımız onluk taban (decimal sistem) dışında farklı sayı sistemleri de vardır. Taban aritmetiği, bilgisayar bilimleri, şifreleme ve kodlama sistemlerinde önemli bir yer tutar.

Temel Sayı Sistemleri:

1. Onluk Taban (Decimal – Tab. 10) → 0,1,2,3,4,5,6,7,8,9 kullanılır.
2. İkilik Taban (Binary – Tab. 2) → 0 ve 1 kullanılır.
3. Sekizlik Taban (Octal – Tab. 8) → 0,1,2,3,4,5,6,7 kullanılır.
4. Onaltılık Taban (Hexadecimal – Tab. 16) → 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F kullanılır.

Taban Sistemi Formülü:
Bir n basamaklı sayının taban değeri b ise, sayının değeri şu şekilde hesaplanır:

Örnek Soru:

(1101)₂ sayısı onluk tabanda kaç eder?
A) 11
B) 12
C) 13
D) 14

Çözüm:

Cevap: C) 13 ✅

AYT Matematik – Sayı Basamakları Deneme Soruları

1. Aşağıdaki sayılardan hangisinin yüzler basamağındaki rakamın basamak değeri 700’dür?

A) 7.345
B) 5.704
C) 6.725
D) 8.173

2. 4.526 sayısının çözümleme işlemi aşağıdakilerden hangisidir?

A) 4.000 + 500 + 20 + 6
B) 4.000 + 52 + 6
C) 4.000 + 520 + 6
D) 4.000 + 50 + 26

3. 3!+4 işleminin sonucu kaçtır?

A) 18
B) 24
C) 30
D) 36

4. (1101)₂ sayısının onluk tabandaki karşılığı kaçtır?

A) 9
B) 11
C) 13
D) 15

5. Aşağıdaki ifadelerden hangisi doğrudur?

A) İki basamaklı en büyük sayı 99’dur.
B) Bir sayının en solundaki rakam her zaman en küçük basamak değerine sahiptir.
C) 0 faktöriyel (0!) tanımsızdır.
D) Bir sayının her basamağı aynı değere sahiptir.

6. Aşağıdaki sayılardan hangisi sekizlik (Octal) sistemde gösterilemez?

7. Bir sayının basamak değeri toplamı o sayıya eşit olduğunda bu sayıya ne ad verilir?

A) Ardışık Sayı
B) Basamak Sayısı
C) Çözümleme Sayısı
D) Tam Sayı

8. İkilik (Binary) sisteminde aşağıdaki sayılardan hangisi geçersizdir?

9. Aşağıdaki ifadelerden hangisi doğrudur?

A) Tüm sayı sistemlerinde en büyük rakam 9’dur.
B) Onluk sistemde yalnızca 10 rakam kullanılır.
C) Sekizlik sistemde 0-8 arasındaki rakamlar kullanılır.
D) İkilik sistemde 0,1 ve 2 kullanılır.

10. Aşağıdaki işlemlerden hangisi doğrudur?

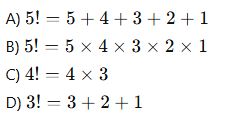
Cevap Anahtarı

1. C
2. A
3. C
4. C
5. A
6. D
7. B
8. C
9. B
10. B